Rigid-body Translational Motion

Newton’s 2nd law states:

$$\begin{array}{rl}m\vec{a}& =\vec{f}\\ m\frac{d\vec{v}}{dt}& =f\end{array}$$

If the mass only moves in the $x$-direction:

$$\begin{array}{rl}v(t)& =\frac{dx(t)}{dt}\\ a(t)& =\dot{v}(t)=\ddot{x}(t)=\frac{d^{2}x(t)}{d{t}^2}\end{array}$$

If we assume:

• The object is rigid
• Can neglect force distribution

Then we can treat the object as a concentrated mass or point mass; the dimensions can be ignored. A lumped element is a point mass.

Mechanical Energy

Conservation of mechanical energy is given by:

$$\begin{array}{r}m\dot{v}=f(x)\end{array}$$

where $v=\frac{dx}{dt}$ and $dx=vdt$. Thus, we can write

$$\begin{array}{rl}m\dot{v}vdt& =f(x)vdt\\ m\frac{dv}{dt}vdt& =vf(x)dt\\ mvdv& =\frac{dx}{dt}f(x)dt\\ mvdv& =f(x)dx\\ \int mvdv& =\int f(x)dxf(x)\\ \underset{\text{Kinetic Energy}}{\underbrace{\frac{1}{2}m{v}^2}}& =\underset{\text{Work}}{\underbrace{\int f(x)dx}}+C\end{array}$$

If the work done by $f(x)$ is independent from the path and only depends on end points, then the force is called a conservative force and can be derived from a function $P(x)$.

$$\begin{array}{rl}f(x)& =-\frac{dP(x)}{dx}\\ \int f(x)dx& =-\int dP(x)\\ P(x)& =-\int f(x)dx\\ \frac{1}{2}m{v}^2& =-P(x)+C\\ \underset{\text{Kinetic energy}}{\underbrace{\frac{1}{2}m{v}^2}}+\underset{\text{Potential Energy}}{\underbrace{P(x)}}& =C\end{array}$$

Let’s say we have a starting time $t_0$. Then, we have:

$$\frac{m{v}_0^2}{2}+P(x_0)=C$$

For an arbitrary time $t$, we then have:

$$\begin{array}{rl}(\frac{m{v}^2}{2}-\frac{m{v}_0^2}{2})+(P(x)-P(x_0))& =0\\ \Delta \text{KE}+\Delta \text{PE}& =0\end{array}$$

Gravity

Gravity is an conservative force:

$$\begin{array}{rl}f& =-mg\\ P(x)& =-\int f(x)dx\\ P(x)& =-\int (-mg)dx\\ P(x)& =mgx\\ \frac{m{v}^2}{2}+mgx& =C\\ \frac{m{v}^2}{2}+\frac{m{v}_0^2}{2}+mg(x-x_0)& =0\end{array}$$

Constant Force

If we have a constant force such that $f(x,t)=f_{\text{constant}}$, we have

$$f(x,t)=u(t)$$

Then, the potential energy is

$$\begin{array}{rl}P(x)& =-\int f(x)dx\\ P(x)& =-\int fdx\\ P(x)& =-f(x)\\ \frac{m{v}^2}{2}-\frac{m{v}_0^2}{2}-f(x-x_0)& =0\\ \underset{\text{KE}}{\underbrace{\frac{m{v}^2}{2}}}& =\underset{\text{Initial KE}}{\underbrace{\frac{m{v}_0^2}{2}}}+\underset{\text{Work done on the mass}}{\underbrace{f(x-x_0)}}\end{array}$$

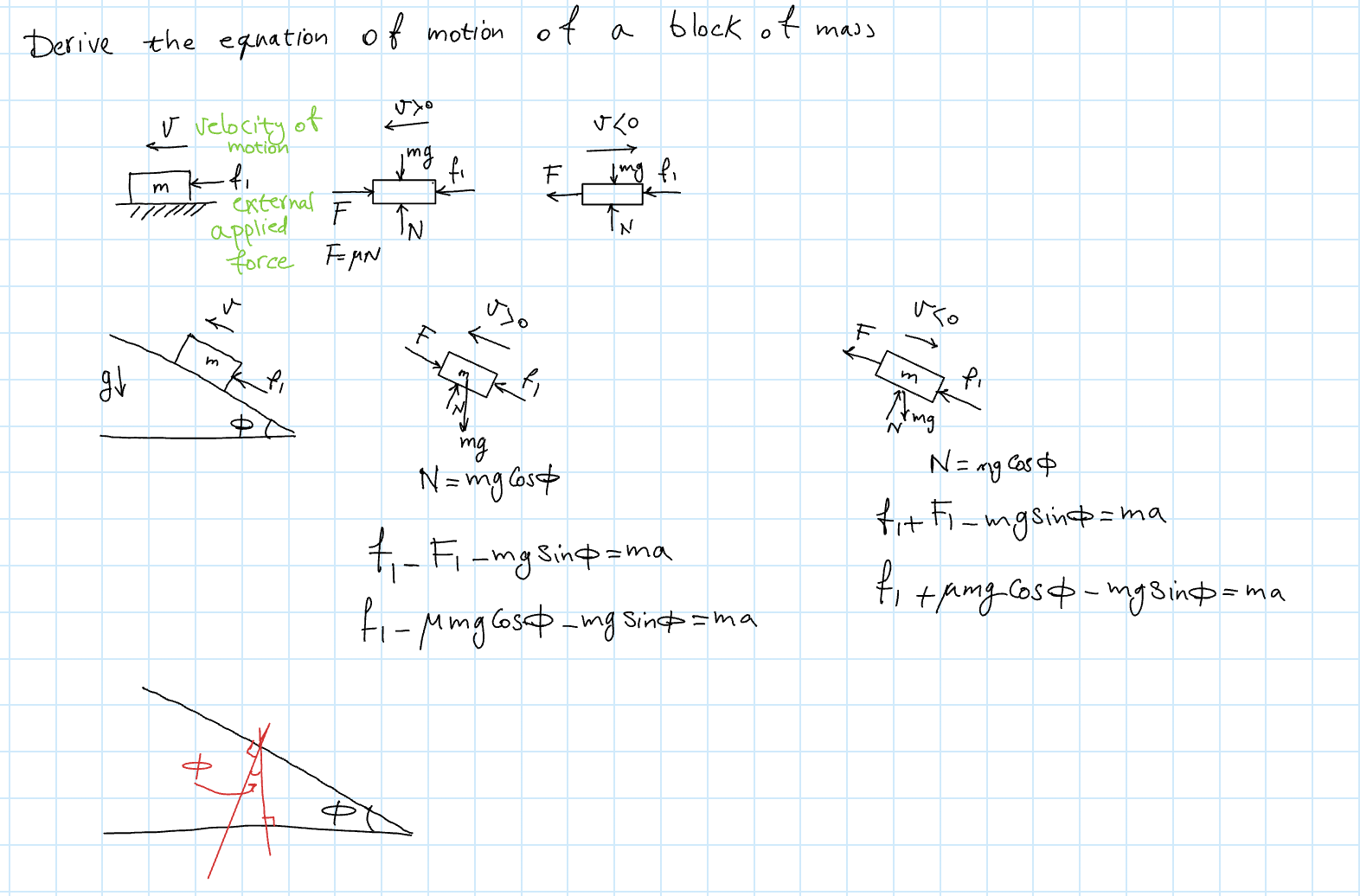
Friction

The work done by friction is path-dependent, so it’s a non-conservative force. We have:

$$F=\mu N$$

where $N$ is the normal force, $\mu$ is the coefficient of friction.

• ${\mu }_s$ is the coefficient of static friction – force required to initiate motion
• ${\mu }_d$ is the coefficient of dynamic friction – force required to maintain motion between two objects in contact

Generally, ${\mu }_s>{\mu }_d$, as it takes more force to start the motion of an object than to keep it moving.