Position and Displacement

The position of a point in the plane can be defined by the use of a position vector. The choice of reference axes is arbitrary and is selected to suit the observer.

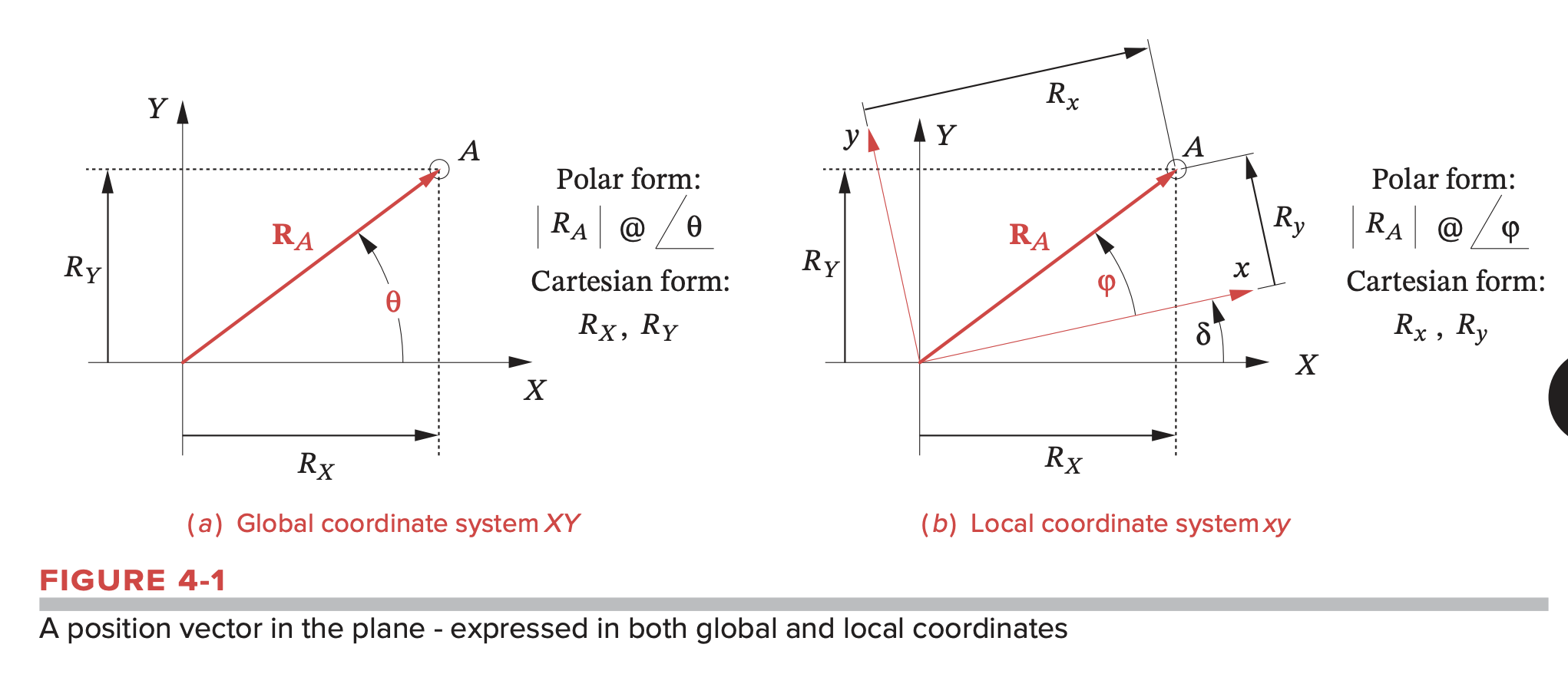
A two-dimensional vector has two attributes, which can be expressed in either polar or cartesian coordinates. The polar form provides the magnitude and the angle of the vector. The cartesian form provides the $X$ and $Y$ components of the vector. Each form is directly convertible into the other by the Pythagorean theorem:

$$R_A=\sqrt{R_X^2+R_Y^2}$$

Coordinate transformation: If the system’s origins are coincident as shown in Figure 4-1b and the required transformation is a rotation, we can transform between the coordinate systems with:

$$\begin{array}{r}{R}_X=R_x\cos \delta -R_y\sin \delta \\ R_Y=R_x\sin \delta +R_y\cos \delta \end{array}$$

Displacement

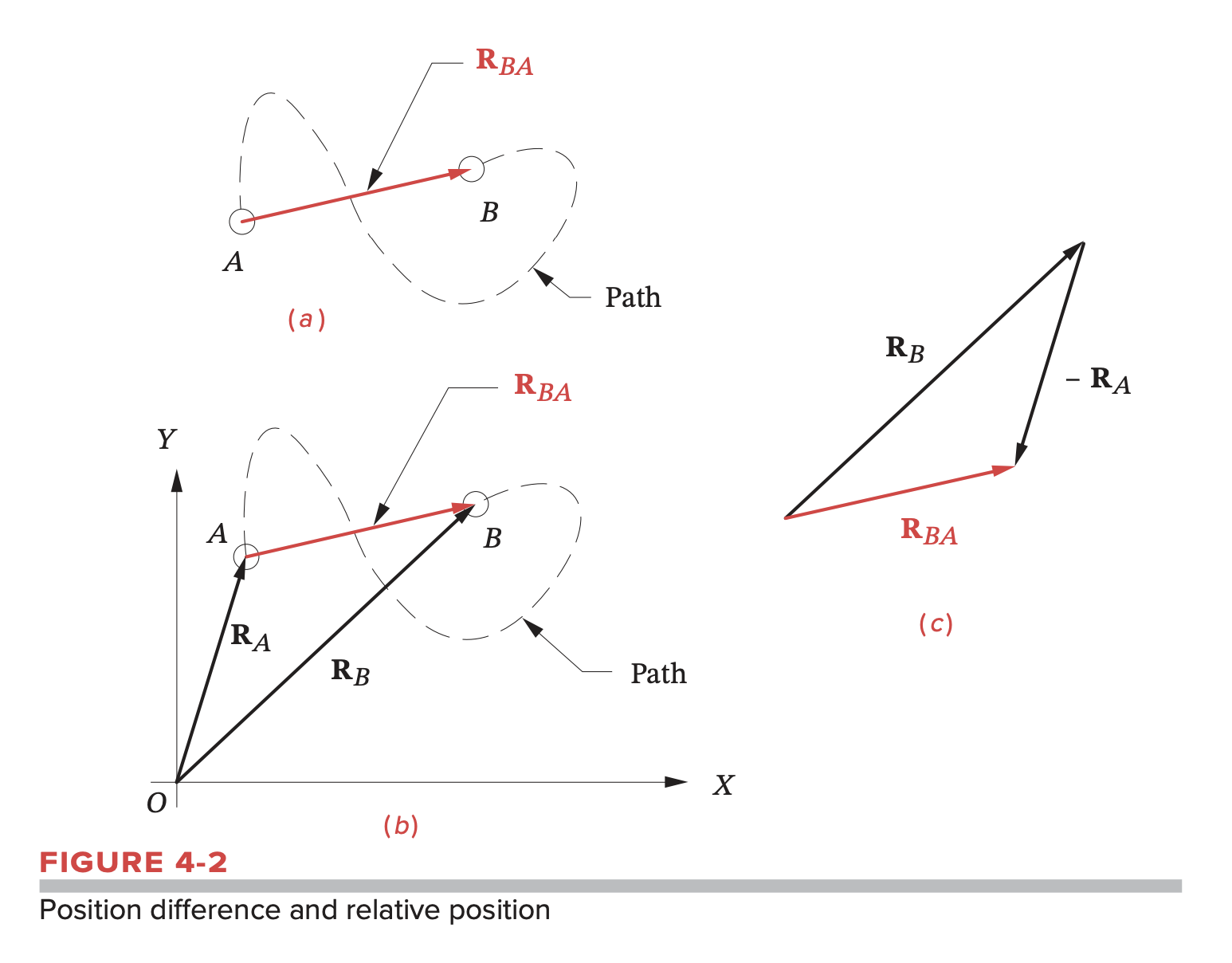
Displacement is the straight-line distance between the initial and final position of a point that has moved in the reference frame. It is not the same as path length.

$$R_{BA}=R_B-R_A$$

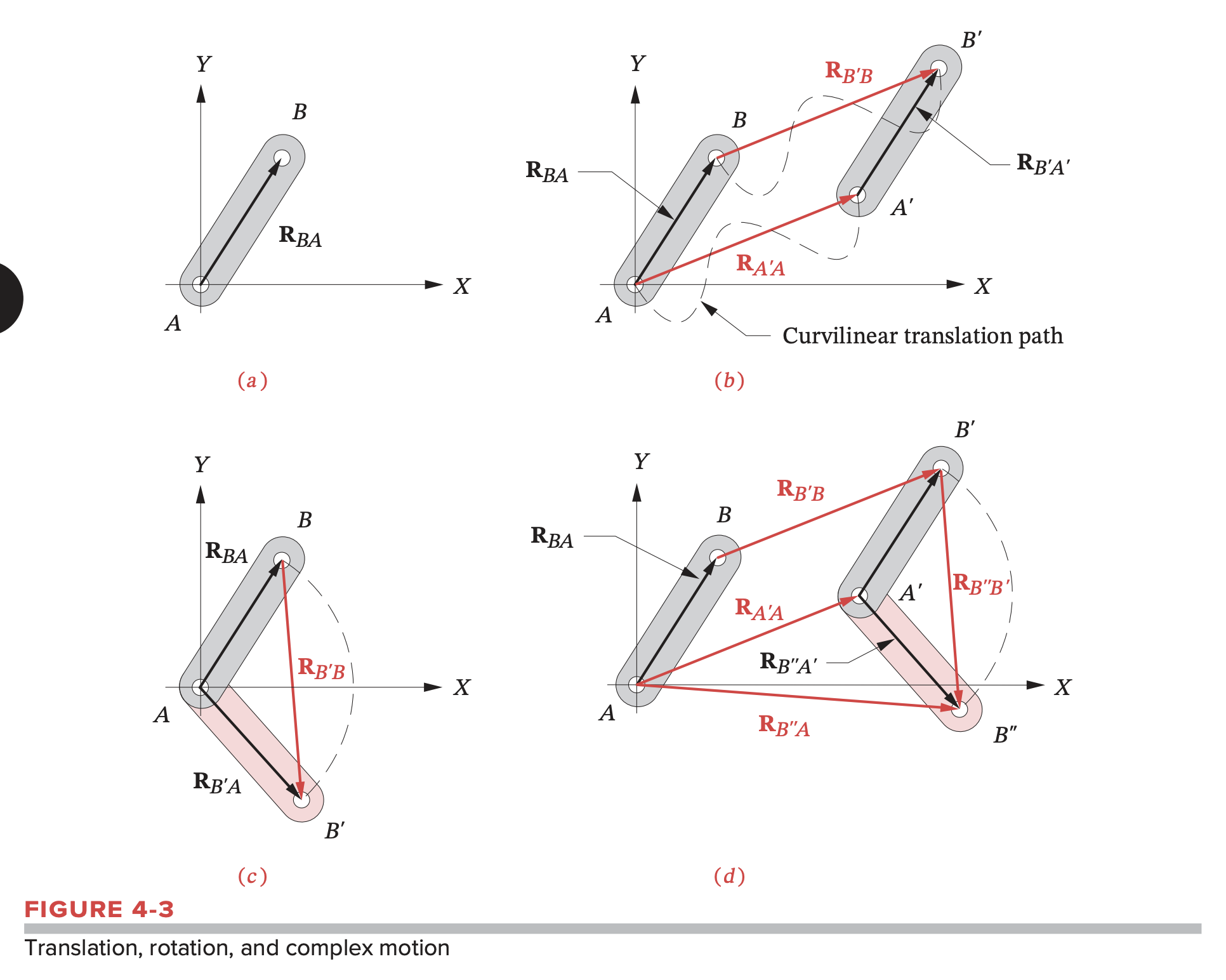
Translation, Rotation, Complex Motion

In translation, all points on the body have the same displacement. As a result, the link retains its angular orientation.

• Note that the translation need not be along a straight path. The curved lines from $A$ to $A’$ and $B$ to $B’$ are the curvilinear translation path of the link. There is no rotation of the link if these paths are parallel.
• If the path happens to be straight, then it will be the special case of rectilinear translation, and the path and the displacement will be the same.

In rotation, different points in the body undergo different displacements and thus there is a displacement difference between any two points chosen. The link now changes its angular orientation in the reference frame, and all points have different displacements.

The general case of complex motion has both translation and rotation components. Note that the order in which these two components are added is irrelevant; the resulting complex displacement will be the same whether you first rotate and then translate or vice versa. This is so because the two factors are independent. The total complex displacement of point $B$ is defined by the following expression

$$\begin{array}{rl}\text{Total displacement}& =\text{Translation component}+\text{Rotation component}\\ R_{B^{\prime \prime }B}& =R_{B^{\prime }B}+R_{B^{\prime \prime }{B}^{\prime }}\end{array}$$

The new absolute position of point B referred to the origin at $A$ is:

$$R_{B^{\prime \prime }A}=R_{A^{\prime }A}+R_{B^{\prime \prime }{A}^{\prime }}$$

These motion states can be expressed as the following theorems.

Euler's Theorem

The general displacement of a rigid body with one point fixed is a rotation about some axis.

Chasles' Theorem

Any displacement of a rigid body is equivalent to the sum of a translation of any one point on that body and a rotation of the body about an axis through that point.