Algebraic Position Analysis

Algebraic position analysis solves the system based on geometry.

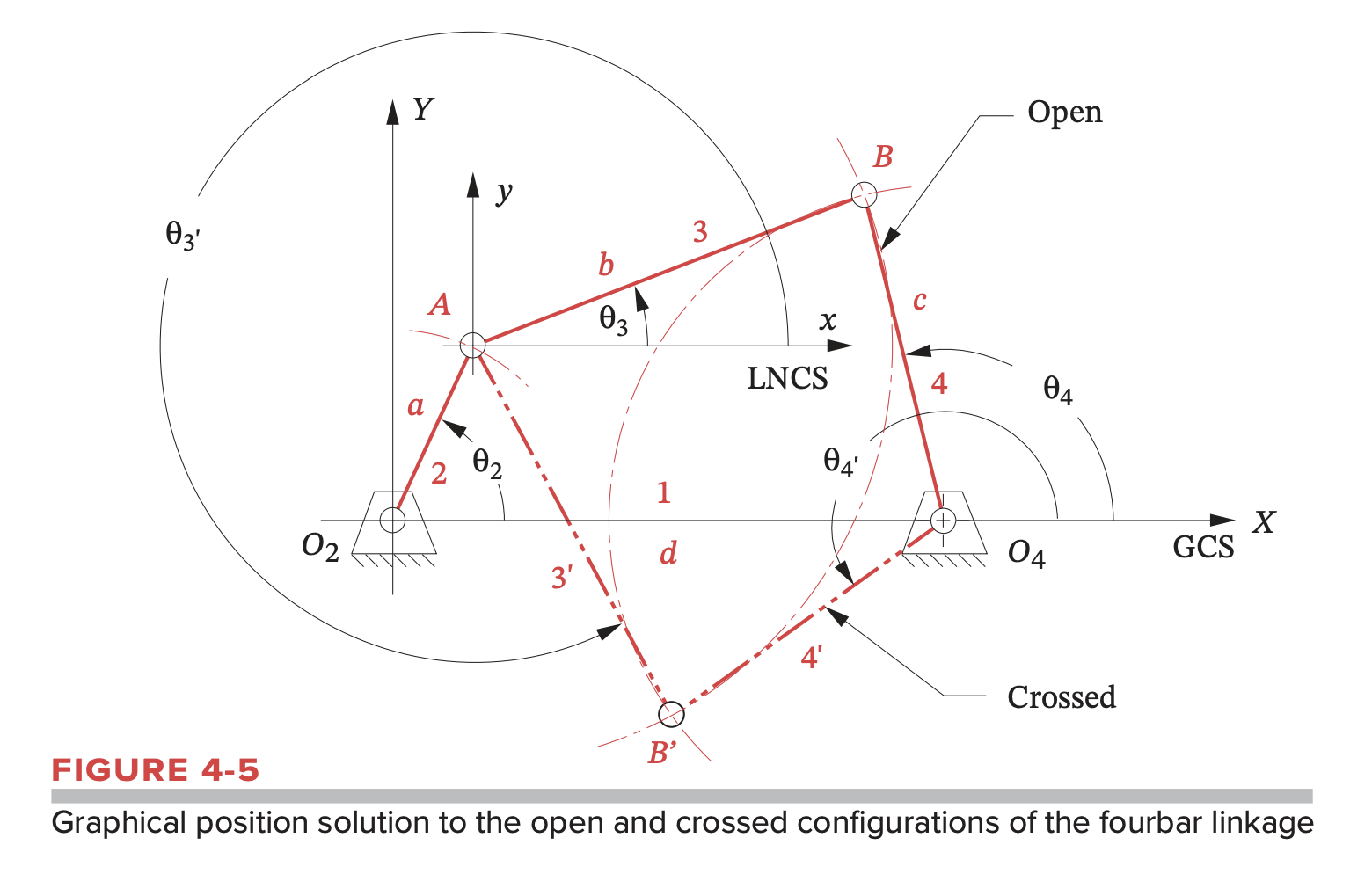
Using the fourbar linkage example above, we would have:

$$\begin{array}{rl}{A}_x& =a\cos {\theta }_2\\ A_y& =a\sin {\theta }_2\end{array}$$

where ${\theta }_2$ is the input angle.

The coordinates of point $B$ are found using the equations of circles about $A$ and $O_4$:

$$\begin{array}{rl}{b}^2& =(B_x-A_x{)}^2+(B_y-A_y{)}^2\\ c^2& =(B_x-d{)}^2+B_y^2\end{array}$$

which provide a pair of simultaneous equations we can solve to get $B_x$ and $B_y$.

Subtracting $b^2-c^2$, we have:

$$\begin{array}{rl}{b}^2-c^2& =(B_x-A_x{)}^2-(B_x-d{)}^2+(B_y-A_y{)}^2-B_y^2\\ & =\cancel{B_x^2}+A_x^2-2B_x{A}_x-(\cancel{B_x^2}+d^2-2d{B}_x)+(\cancel{B_y^2}+A_y^2-2B_y{A}_y)-\cancel{B_{y^2}}\\ & =\underset{a^2}{\underbrace{A_x^2+A_y^2}}-2A_x{B}_x-2A_y{B}_y-d^2\\ a^2-b^2+c^2-d^2& =2A_x{B}_x+2A_y{B}_y-2d{B}_x\\ B_x& =\frac{a^2-b^2+c^2-d^2}{2(A_x-d)}-\frac{2A_y{B}_y}{2(A_x-d)}\end{array}$$

We can do similar calculations for $B_y$. This gives us

$$\begin{array}{rl}{B}_x& =S-\frac{2A_y{B}_y}{2(A_x-d)}\\ B_y& =\frac{-Q\pm \sqrt{Q^2-4PR}}{2P}\end{array}$$

where

$$\begin{array}{rl}S& =\frac{a^2-b^2+c^2-d^2}{2(A_x-d)}\\ R& =(d-S{)}^2-c^2\\ P& =\frac{A_y^2}{(A_x-d{)}^2}+1\\ Q& =\frac{2A_y(d-S)}{A_x-d}\end{array}$$

The solutions to this equation set can be real or imaginary. If imaginary, the links cannot connect at the given input angle or at all. Once the two values of By are found (if real), they can be substituted into equation 4.2d to find their corresponding x components.

We can use these values to find the link angles:

$$\begin{array}{rl}{\theta }_3& ={\tan }^{-1}\left(\frac{B_y-A_y}{B_x-A_x}\right)\\ {\theta }_4& ={\tan }^{-1}\left(\frac{B_y}{B_x-d}\right)\end{array}$$

Like the fourbar example above, we can do this type of analysis for all types of mechanisms.