Types of Errors

Round-Off Errors

When numbers with limited significant digits are used to represent exact numbers.

Scientific notation:

$$m\cdot b^e$$

where:

• $m$ = mantissa
• $b$ = base of number system being used
• $e$ = exponent Example: $1.23\cdot 10^4$

Computer round-off errors:

• Overflow error – numbers are too large or too small to be represented
• Quantizing errors – irrational numbers cannot be entirely represented (e.g. $\pi$)
• Error in interval between numbers (when $\Delta x$ increases as the number grows, the floating point representation can keep its significant digits, but the quantizing errors will be proportional to the magnitude of the number)
  • Machine epsilon – ratio of $\Delta x$ to $x$
  • Relative approximate error due to rounding numbers

Truncation Errors

From use of approximation in place of exact mathematical procedure.

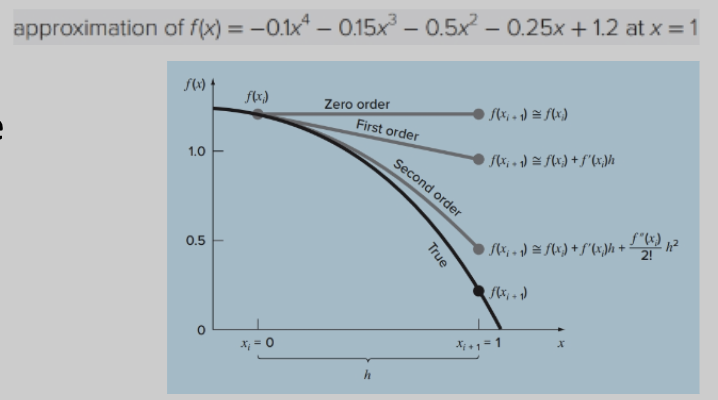
For example, using $\frac{dv}{dt}=\frac{\Delta v}{\Delta t}$ Can be expressed in terms of Taylor Series:

• If a function $f$ and its first $n+1$ derivatives are continuous on an interval of width $h$ containing $x$, then the value of the function at $x+h$ is given by:

$$\begin{array}{rl}f(x_{i+1})& =f(x_i)+f^{\prime }(x_i)h+\frac{f^{\prime \prime }(x_i)h^2}{2!}\dots \\ h& =x_{i+1}-x_i\end{array}$$

This relates the value of the function $x_{i+1}$ to $x_i$.

So, we have:

$$\underset{\text{Exact}}{\underbrace{\frac{df(x_i)}{dx}}}=\underset{\text{Approximation}}{\underbrace{\frac{f(x_{i+1})-f(x_i)}{h}}}-\underset{\text{Higher-order terms truncation error}}{\underbrace{\frac{h}{2!}{f}^{\prime \prime }(x_i)-\frac{h^2}{3!}{f}^{\prime \prime \prime }(x_i)-\dots }}$$

Since we typically have $h\ll 1$, we have:

• $\frac{h}{2!}{f}^{\prime \prime }(x_i)\gg \frac{h^2}{3!}{f}^{\prime \prime \prime }(x_i)$ and other higher-order terms
• Truncation error of order $h$ is referred to as “first-order”
• Truncation error is the difference between the true value of a function, and the value obtained from numerical approximation.