n-dimensional Spaces

To define the higher-dimensional analogues of ${\mathbb{R}}^2$ and ${\mathbb{R}}^3$, we will simply replace $\mathbb{R}$ with $\mathbb{F}$ (which equals $\mathbb{R}$ and $\mathbb{C}$ as defined here), and replace $2$ and $3$ with an arbitrary positive integer.

We define ${\mathbb{F}}^n$ to be the set of all lists of length $n$ of elements of $\mathbb{F}$:

$${\mathbb{F}}^n=\{(x_1,\dots ,x_n):x_k\in \mathbb{F}\text{ for }k=1,\dots ,n\}.$$

For $(x_1,\dots ,x_n)\in {\mathbb{F}}^n$ and $k\in \{1,\dots ,n\}$, we say that $x_k$ is the $k$th coordinate of $(x_1,\dots ,x_n)$.

Example: 4D complex space

For example ${\mathbb{C}}^4$ is the set of all lists of four complex numbers:

$${\mathbb{C}}^4=\{(z_1,z_2,z_3,z_4):z_1,z_2,z_3,z_4\in \mathbb{C}\}.$$

If $n\ge 4$, we cannot visualize ${\mathbb{R}}^n$ as a physical object. Similarly, ${\mathbb{C}}^1$ can be thought of as a plane, but for $n\ge 2$, the human brain cannot provide a full image of ${\mathbb{C}}^n$. However, even if $n$ is large, we can perform algebraic manipulations in ${\mathbb{F}}^n$ as easily as in ${\mathbb{R}}^2$ or ${\mathbb{R}}^3$.

Addition

For example, we can define addition in ${\mathbb{F}}^n$ is defined by adding corresponding coordinates:

$$(x_1,\dots ,x_n)+(y_1,\dots ,y_n)=(x_1+y_1,\dots ,x_n+y_n).$$

We can simplify the notation to just use one letter, such as just $x$ and $y$ instead of using $(x_1,\dots ,x_n)$ and $(y_1,\dots ,y_n)$.

• If a single letter is used to denote an element of ${\mathbb{F}}^n$, then the same letter with appropriate subscripts is often used when coordinates must be displayed.
• For example, if $x\in {\mathbb{F}}^n$, then letting $x$ equal $(x_1,\dots ,x_n)$ is good notation, as shown in the proof below.
• Even better, we will work with just $x$ and avoid explicit coordinates when possible.

Proof: Commutativity of addition

If $x,y\in {\mathbb{F}}^n$, then $x+y=y+x$.

Suppose that $x=(x_1,\dots ,x_n)\in {\mathbb{F}}^n$ and $y=(y_1,\dots ,y_n)\in {\mathbb{F}}^n$. Then

$$\begin{array}{rl}x+y& =(x_1,\dots ,x_n)+(y_1,\dots ,y_n)\\ & =(x_1+y_1,\dots ,x_n+y_n)\\ & =(y_1+x_1,\dots ,y_n+x_n)\\ & =(y_1,\dots ,y_n)+(x_1,\dots ,x_n)\\ & =y+x\end{array}$$

where:

• the second and fourth equalities holds because of the definition of addition in ${\mathbb{F}}^n$
• the third equality holds because of the usual commutativity of addition in $\mathbb{F}$.

Q.E.D.

Definition of Zero

Let $0$ denote the list of length $n$ whose coordinates are all $0$:

$$0=(0,\dots ,0)$$

• On the left side, the symbol $0$ denotes a list of length $n$, which is an element of ${\mathbb{F}}^n$.
• On the right side, each $0$ denotes a number.

Geometric Intuition

A typical element of ${\mathbb{R}}^2$ is a point $v=(a,b)$. Sometimes we think of $v$ not as a point but as an arrow starting at the origin and ending at $(a,b)$, as shown here. When we think of an element of ${\mathbb{R}}^2$ as an arrow, we refer to it as a vector.

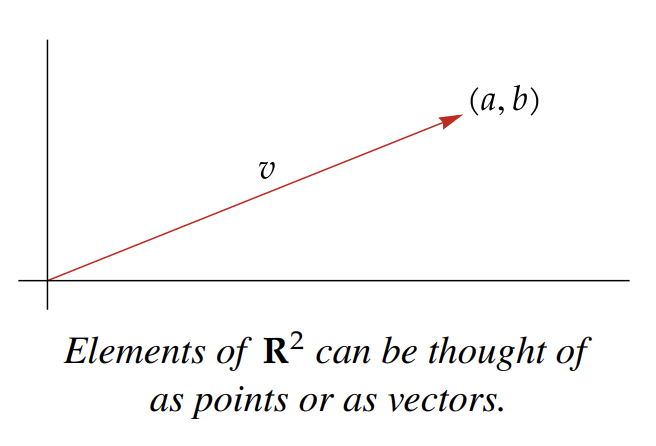
When we think of vectors in ${\mathbb{R}}^2$ as arrows, we can move an arrow parallel to itself (not changing its length or direction) and still think of it as the same vector. With that viewpoint, you will often gain better understanding by dispensing with the coordinate axes and the explicit coordinates and just thinking of the vector, as shown in the figure here.

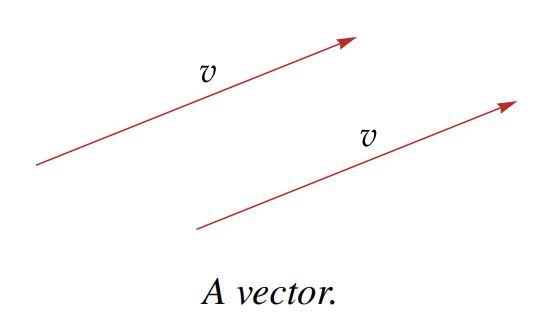
• The two arrows shown here have the same length and same direction, so we think of them as the same vector.

Whenever we use pictures in ${\mathbb{R}}^2$, or use the somewhat vague language of points and vectors, remember that these are just aids to our understanding, not substitutes for the actual mathematics that we will develop. Although we cannot draw good pictures in high-dimensional spaces, the elements of these spaces are as rigorously defined as elements of ${\mathbb{R}}^2$.

For example, $(2,-3,17,\pi ,\sqrt{2})$ is an element of ${\mathbb{R}}^5$, and we may casually refer to it as a point in ${\mathbb{R}}^5$ or a vector in ${\mathbb{R}}^5$, without worrying about whether the geometry of ${\mathbb{R}}^5$ has any physical meaning.

Geometric Intuition for Addition

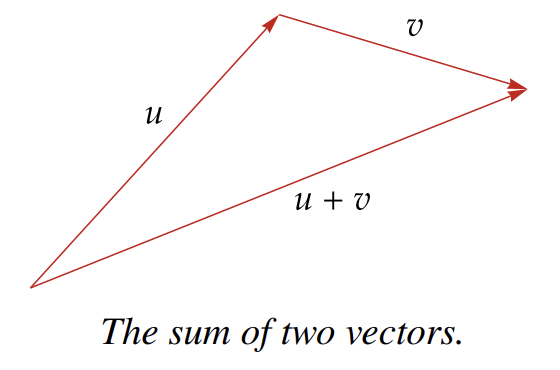
Recall that we defined the sum of two elements of ${\mathbb{F}}^n$ to be the element of ${\mathbb{F}}^n$ obtained by adding corresponding coordinates. As we will now see, addition has a simple geometric interpretation in the special case of ${\mathbb{R}}^2$.

Suppose we have two vectors $u$ and $v$ in ${\mathbb{R}}^2$ that we want to add. Move the vector $v$ parallel to itself so that its initial point coincides with the end point of vector $u$, as shown here. The sum $u+v$ then equals the vector whose initial point of $u$ and whose end point equals the end point of $v$, as shown here.

Additive Inverse

We can continue to define more operations in ${\mathbb{F}}^n$, and look at the accompanying geometric interpretation in ${\mathbb{R}}^2$.

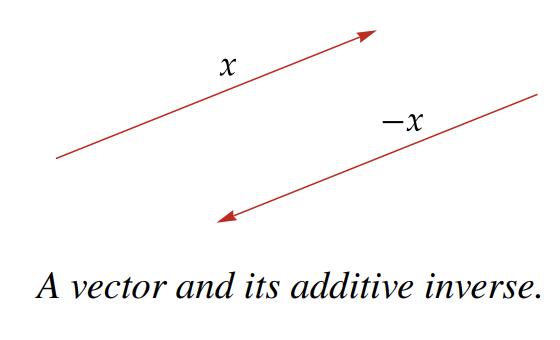
Definition: Additive Inverse

For $x\in {\mathbb{F}}^n$, the additive inverse of $x$, denoted by $-x$, is the vector $-x\in {\mathbb{F}}^n$ such that

$$x+(-x)=0$$

Thus, if $x=(x_1,\dots ,x_n)$, then $-x=(-x_1,\dots ,-x_n)$.

Geometrically, the additive inverse of a vector in ${\mathbb{R}}^2$ is the vector with the same length but pointing in the opposite direction.

Scalar Multiplication

Scalar multiplication will be central to our subject. Specifically, we need to define what it means to multiply an element of ${\mathbb{F}}^n$ by an element of $\mathbb{F}$.

Definition: Scalar Multiplication

The product of a number $\lambda$ and a vector in ${\mathbb{F}}^n$ is computed by multiplying each coordinate of the vector by $\lambda$:

$$\lambda (x_1,\dots ,x_n)=(\lambda x_1,\dots ,\lambda x_n)$$

Here, $\lambda \in \mathbb{F}$ and $(x_1,\dots ,x_n)\in {\mathbb{F}}^n$.

Scalar multiplication has a nice geometric interpretation in ${\mathbb{R}}^2$. If $\lambda >0$ and $x\in {\mathbb{R}}^2$, $\lambda x$ is the vector that points in the same direction as $x$ and whose length is $\lambda$ times the length of $x$. In other words, to get $\lambda x$, we shrink or stretch $x$ by a factor of $\lambda$, depending on whether $\lambda <1$ or $\lambda >1$.

If $\lambda <0$ and $x\in {\mathbb{R}}^2$, then $\lambda x$ is the vector that points in the opposite direction to that of $x$ and whose length is $|\lambda |$ times the length of $x$.