One-sided Binary Search

This is a common variation of a binary search, and is often used in binary search-related problems.

Problem

An array of boolean values is divided into two sections; the left section consists of all false and the right section consists of all true. Find the First True in a Sorted Boolean Array of the right section, i.e. the index of the first true element. If there is no true element, return -1.

Solution

• Time complexity $O(\log n)$
• Space complexity $O(1)$

from typing import List
 
def find_boundary(arr: List[bool]) -> int:
    
    l, r = 0, len(arr) - 1
    boundary = -1
    
    while l <= r:
        
        m = (l+r) // 2
        
        if arr[m] == False:
            l = m + 1
        elif arr[m] == True:
            r = m - 1
            boundary = m
    return boundary
        
if __name__ == '__main__':
    arr = [x == "true" for x in input().split()]
    res = find_boundary(arr)
    print(res)

Here, we update l and r just like a numerical binary search. For the right case there’s a difference:

• If the current element is true, the current element could be the first true although there may be other true to the left.
• Thus, after we discard everything to the right (by updating r) and store the current element.

Alternate Solution

Another approach to handle the right side case above is to keep the current element in the search range instead of discarding it, doing if arr[mid]: right = mid instead of right = mid - 1.

• However, doing this without modifying the while condition will result in an infinite loop. This is because when left == right, right = mid will not modify right. So, the search range doesn’t shrink and we will be stuck in the while loop forever.
• To make this work, we have to remove the equality in the while condition. In addition, as mentioned in the last module, a while loop without equality will miss the single-element edge case so we have to add an additional check after the loop to handle this case.
• Overall, we have to make three modifications to the vanilla binary search to make it work.

Using with “feasible”

To use binary search, we must be dealing with some monotonic function – in this case, a monotonic function that either returns True or False. We can design a feasible function to signify whether the element at the current index is feasible (True) or not (False) to meet the problem constraints.

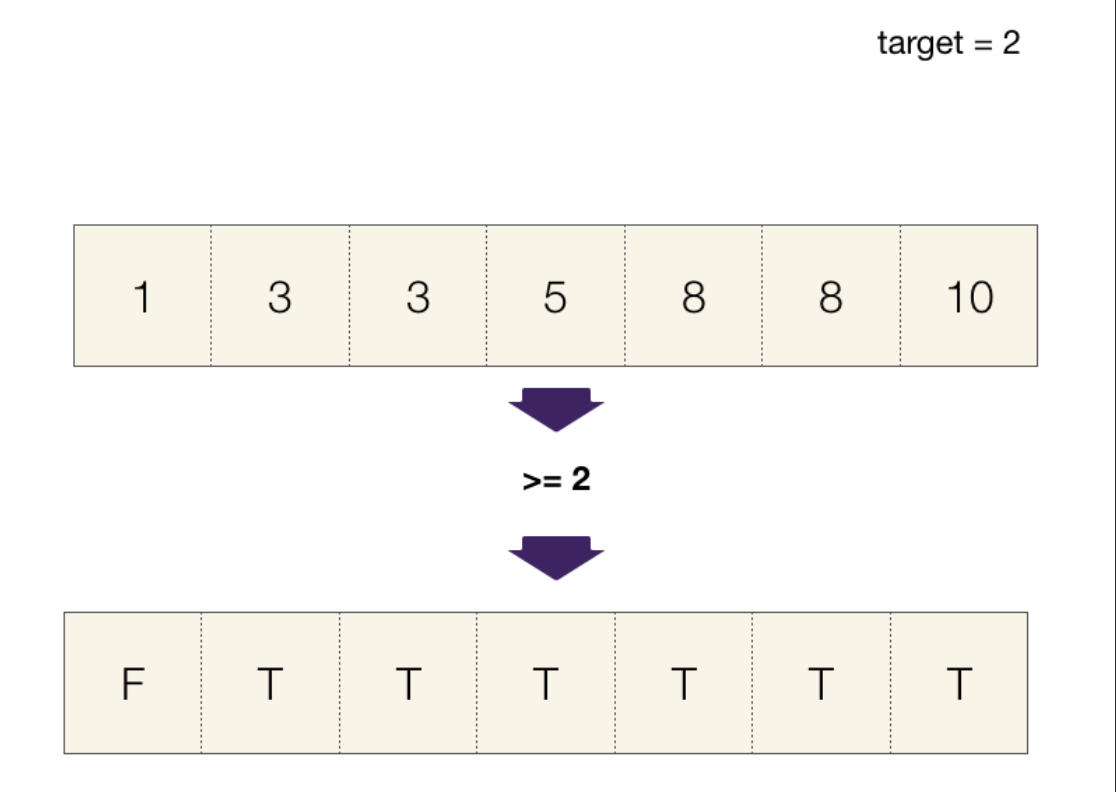
Example: First Element Not Smaller Than Target

Given an array of integers sorted in increasing order and a target, find the index of the first element in the array that is larger than or equal to the target. Assume that it is guaranteed to find a satisfying number.

• Input:
  • arr = [1, 3, 3, 5, 8, 8, 10]
  • target = 2
• Output: 1

The problem is equivalent to finding the boundary of elements less than 2 and elements larger than or equal to 2 in the sorted array. Because the array is sorted, as the index increases, once we see an element greater than 2, the rest of the array should also be greater than 2. This is a monotonic function. The feasible function here is arr[i] >= target.

def first_not_smaller(arr: List[int], target: int) -> int:
	left, right = 0, len(arr) - 1
	boundary_index = -1
	while left <= right:
		mid = (left + right) // 2
		if arr[mid] >= target:
			boundary_index = mid
			right = mid - 1
		else:
			left = mid + 1
	return boundary_index

This is the exact same as binary search for boolean array, except we changed the condition to arr[mid] >= target.

Example: Find Element in Sorted Array with Duplicates

Given a sorted array of integers and a target integer, find the first occurrence of the target and return its index. Return -1 if the target is not in the array.

• Input:
  • arr = [1, 3, 3, 3, 3, 6, 10, 10, 10, 100]
  • target = 3
• Output: 1

def find_first_occurrence(arr: List[int], target: int) -> int:
    l, r = 0, len(arr) - 1
    ans = -1
    
    while l <= r:
        
        m = (l + r) // 2
        
        if arr[m] == target:
            r = m - 1
            ans = m
        elif arr[m] < target:
            l = m + 1
        elif arr[m] > target:
            r = m - 1
    
    return ans

The feasible function is arr[i] >= target. However, the question wants the index of the first element exactly equal to the target.

• Our template updates ans = mid whenever arr[mid] >= target.
• Therefore we have to make a small modification to the template and move ans = mid to only when arr[mid] == target and not arr[mid] >= target.