Trajectory-based metaheuristics explore the search space by iteratively transforming a single incumbent solution according to problem-depending neighborhood structures and high-level strategies.
- Operate on a single solution trajectory
- Replace exhaustive enumeration by guided motion
- Balance intensification and diversification
Some representative methods:
Tree Search vs. Trajectory Search
Tree search (BFS/UCS/A*/Minimax):
- Maintains a frontier of many partial states
- Explores branches of a state space tree
- Can be complete/optimal if resources allow
Trajectory search (local search/SA/Tabu):
- Maintains one current solution
- Repeatedly applies a move operator to get a neighbor
- Trades guarantees for scalability on huge spaces
For many combinatorial methods, the branching factor is large and the depth is large. For example, for the Traveling Salesman Problem, the number of tours would be , so it’s not feasible to explore all of them.
Trajectory Search Ingredients
Trajectory methods replace trees with motion on a landscape. A trajectory algorithm is defined by four coupled choices:
- Representation : Encodes a complete candidate solution
- Cost energy function : Defines an optimization objective, inducing a landscape over the solution space
- Neighborhood structure : Defines how the algorithm can move, encoding problem structure and constraints
- Acceptance rule: Decides whether to move to a worse, equal, or better neighbor. This is usually the main lever for escaping local minima
TSP Example
Given a Traveling Salesman Problem, where we want to visit each city once, return to the starting city, and minimize the total tour length.
The solution representation can be given by a permutation .
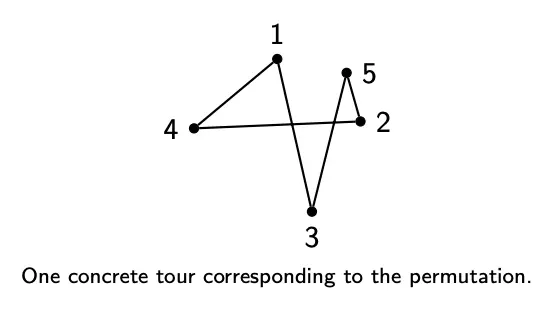
The cost/energy function can be the total tour length.
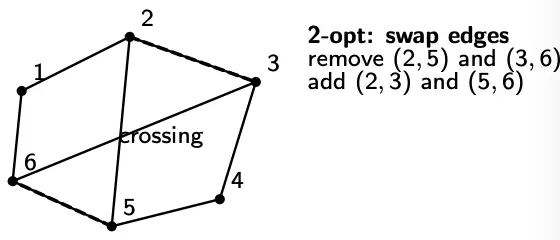
The neighborhood can be 2-opt swaps of a tour.