Minimax

Minimax is a decision rule for minimizing the possible loss for a worst case (maximum loss) scenario. When dealing with gains, it is refered to as maximin (to maximize the minimum gain). It was originally formulated for two-player zero-sum games.

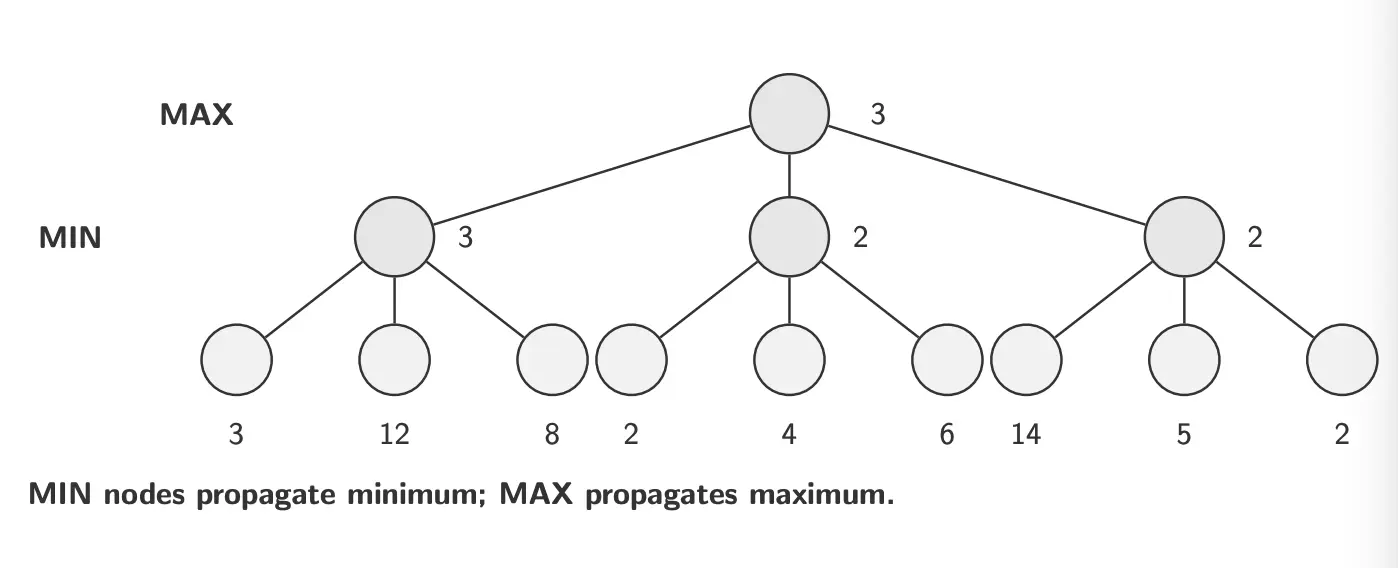
Given a game tree, the optimal strategy can be determined by examining the minimax value of each node, which we write as $\text{MINIMAX-VALUE}(n)$. The minimax value of a node is the utility of being in the corresponding state, assuming that both players play optimally from there to the end of the game. The minimax value of a terminal state is just its utility.

In general, we go through this process:

• Label each level in the game tree with MAX (player) or MIN (opponent)
• Label leaves with evaluation of the player
• Go through the game tree:
  • If parent node is MAX, label the node with the maximum value of its successors
  • If parent node is MIN, label the node with the minimum value of its successors

Limited Depth and Evaluation Function

Expanding the complete game tree is only feasible for simple games, as we saw in Minimax Tic-Tac-Toe Example. For more complex games like chess, it’s only feasible to explore a limited depth of the game tree and use a board evaluation function to estimate the worth of this node to the player.

Properties

• Complete: Yes, if the game tree is finite and explored to terminal states
• Optimal: Yes, assuming an optimal/rational opponent
• Time complexity: $O(b^d)$ where $b$ is the branching factor and $d$ is the depth of the game tree
• Space complexity: $O(bd)$ due to depth-first traversal of the game tree

Limitations: Exponential time complexity makes full minimax infeasible for large games, motivating depth-limited search and heuristic evaluation functions.w