MTE 484 Lab 3

Outer loop sampling time

$${\omega }_0=\frac{2\pi }{7}=0.897597901$$ $${\omega }_{bw}=\text{max}(\text{Re}(p_i))=59.5291$$ $$\begin{array}{rl}{\omega }_s& >5\times \text{max}\{{\omega }_{bw},{\omega }_0\}\\ & >5\times 59.5291\\ & >297.6455\end{array}$$ $$T>\frac{2\pi }{297.6455}>0.02110962641=22\text{ ms}$$

Plant:

$$K_2\cdot \frac{K_3}{s^2}=\frac{-0.293675}{s^2}$$ $$\begin{array}{r}\frac{-0.00809z-0.00809}{(z-1{)}^2}\\ =-\frac{0.00809}{z-1}-\frac{0.01618}{(z-1{)}^2}\end{array}$$

W:

X:

So D = W/X:

NOTE

Yes, I can walk you through exactly how to go from those W and X to a controller

D(z) = \frac{W(z)}{X(z)}

and then into the polynomial / tf(‘z^-1’) form.

---

1. Write W and X explicitly

From your MATLAB output: W:

$$W(z)=\frac{-4.3847(z-1{)}^2(z^2-1.839z+0.8462)(z^2-0.5099z+0.2786)}{(z-0.8)(z^2-1.792z+0.8059)(z^2-0.5752z+0.09092)(z^2-1.194z+0.4535)}$$

X:

$$X(z)=\frac{(z-1{)}^2(z-0.9069)(z^2-0.3848z+0.07871)(z^2-1.069z+0.4896)}{(z-0.8)(z^2-1.792z+0.8059)(z^2-0.5752z+0.09092)(z^2-1.194z+0.4535)}$$

Both are discrete-time, sample time 0.2 s, zpk models.

2. Form the controller D = W/X By definition:

$$D(z)=\frac{W(z)}{X(z)}=\frac{{\text{num}}_W(z)}{{\text{den}}_W(z)}/\frac{{\text{num}}_X(z)}{{\text{den}}_X(z)}=\frac{{\text{num}}_W(z){\text{den}}_X(z)}{{\text{den}}_W(z){\text{num}}_X(z)}$$

But here ${\text{den}}_W(z)={\text{den}}_X(z)$, so they cancel, and you also have a common (z-1)^2 that cancels:

$$\begin{array}{rl}D(z)& =\frac{-4.3847(z-1{)}^2(z^2-1.839z+0.8462)(z^2-0.5099z+0.2786)}{(z-1{)}^2(z-0.9069)(z^2-0.3848z+0.07871)(z^2-1.069z+0.4896)}\\ & =-4.3847\frac{(z^2-1.839z+0.8462)(z^2-0.5099z+0.2786)}{(z-0.9069)(z^2-0.3848z+0.07871)(z^2-1.069z+0.4896)}.\end{array}$$

That’s your controller in factored z-form.

In MATLAB, you can literally do:

D = minreal(W / X);      % zpk controller
zpk(D)                   % to see the same factorized form

3. Expand to numerator & denominator polynomials in z

Now expand the polynomials (I’ve done the algebra for you): Numerator N(z)

$$N(z)=-4.3847(z^2-1.839z+0.8462)(z^2-0.5099z+0.2786)$$

Expanding gives:

$$N(z)=-4.3847z^4+10.29922183z^3-9.04347049667z^2+4.138379743466z-\mathrm{1.033698812804.}$$

Denominator D(z)

$$D(z)=(z-0.9069)(z^2-1.069z+0.4896)(z^2-0.3848z+0.07871)$$

Expanding gives:

D(z) = z^5 - 2.3607,z^4 + 2.29811242,z^3 - 1.16099381228,z^2 + 0.285702098583,z - 0.0349486756704.

So as a transfer function in powers of z:

D(z) = \frac{-4.3847 z^4 + 10.29922183 z^3 - 9.04347049667 z^2 + 4.138379743466 z - 1.033698812804} {z^5 - 2.3607 z^4 + 2.29811242 z^3 - 1.16099381228 z^2 + 0.285702098583 z - 0.0349486756704}.

In MATLAB:

num_z = [-4.3847, 10.29922183, -9.04347049667, 4.138379743466, -1.033698812804];
den_z = [1, -2.3607, 2.29811242, -1.16099381228, 0.285702098583, -0.0349486756704];

Dz = tf(num_z, den_z, 0.2);   % variable is z (implicitly)

---

4. Convert to z^{-1} form for 

tf(‘z^-1’)

Simulink’s Discrete Transfer Fcn (with ‘variable’,‘z^-1’) wants polynomials in z^{-1}:

D(z) = \frac{a_0 + a_1 z^{-1} + \dots + a_m z^{-m}} {b_0 + b_1 z^{-1} + \dots + b_n z^{-n}}.

If the polynomial in z is

• numerator: n_0 z^4 + n_1 z^3 + \dots + n_4

• denominator: d_0 z^5 + d_1 z^4 + \dots + d_5,

then the coefficients in z^{-1} order are just the reversed vectors:

• numerator in z^{-1}: [n_4, n_3, n_2, n_1, n_0]

• denominator in z^{-1}: [d_5, d_4, d_3, d_2, d_1, d_0]

So for your controller:

num_z = [-4.3847,       10.29922183,     -9.04347049667, ...
          4.138379743466, -1.033698812804];

den_z = [ 1.0,          -2.3607,         2.29811242, ...
         -1.16099381228, 0.285702098583, -0.0349486756704];

% Reverse to get z^-1 coefficients
aD = fliplr(num_z);
bD = fliplr(den_z);

Numerically (rounded a bit):

aD = [-1.033699,  4.138380, -9.043470, 10.299222, -4.384700];
bD = [-0.034949,  0.285702, -1.160994,  2.298112, -2.360700, 1.000000];

Dz_inv = tf(aD, bD, 0.2, 'variable', 'z^-1');

Now Dz_inv is exactly the same controller as D = W/X, but in the form you can drop directly into a Discrete Transfer Fcn block (or use in your MATLAB code the same way you’ve been doing for Dzinv_outer/Dzinv_inner.

---

Summary of the process

1. Start from zpk forms of W and X.

2. Form the controller: D = minreal(W/X);.

3. Either:

   • Use zpk(D) to see factored form, or

   • Use tf(D) → tfdata to get polynomial in z, then reverse the coefficient vectors to get z^{-1} form.

4. Use those reversed coefficients in tf(…,‘variable’,‘z^-1’).

If you paste your actual MATLAB variables for W and X, I can write the exact 3–4 lines you’d run to get D in the same style as your existing lab code.

7-pole Solution

12-pole Solution

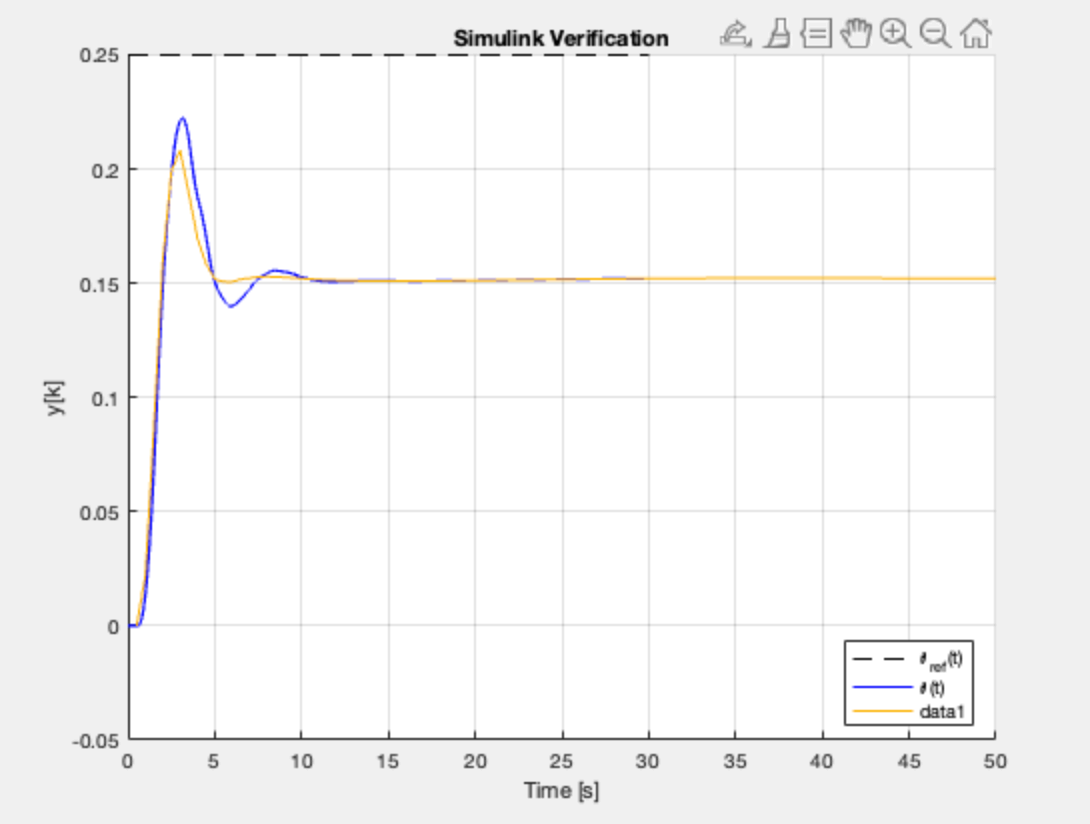
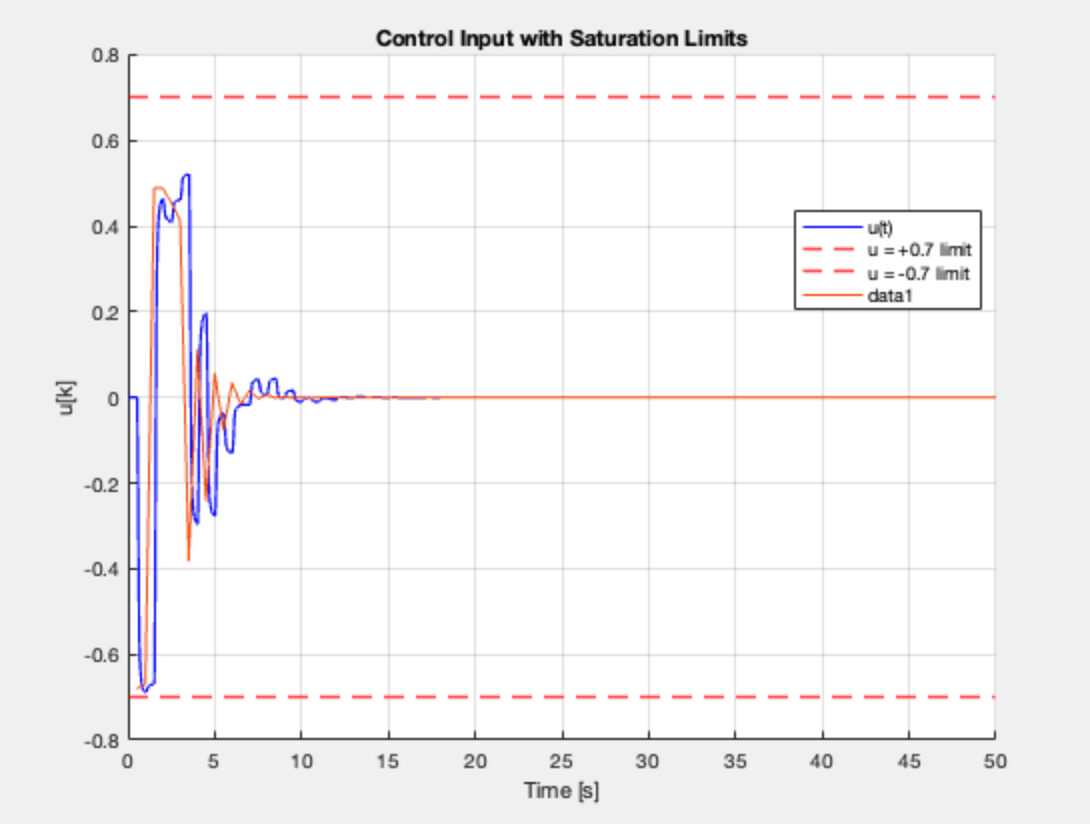
T = 0.25

T = 0.25;

realWPoles = [0.9];
complexWPoles = generate_poles(10, 0.4, 0.5);

--- stepinfo results ---
Rise time:        0.8971 s
Settling time:    11.8056 s
Overshoot:        57.48 %
Peak value:       0.232584
Peak time:        3.1250 s (relative to step)
Max absolute control input (outer loop): 0.695026

   -4.5825 (z-0.8247) (z+0.3899) (z^2 - 1.953z + 0.9543) (z^2 - 1.626z + 0.6638) (z^2 - 1.783z + 0.8003) (z^2 - 1.15z + 0.389) 
(z^2 - 1.495z + 0.6256) (z^2 - 1.656z + 0.8219) (z^2 - 0.9419z + 0.381) (z^2 - 0.8224z + 0.9614)
  -----------------------------------------------------------------------------------------------------------------------------------------
  (z-0.9314) (z-0.9825) (z+0.01767) (z^2 - 1.602z + 0.6437) (z^2 - 1.755z + 0.7744) (z^2 - 1.15z + 0.389) (z^2 - 1.495z + 0.6255) 
(z^2 - 1.617z + 0.783) (z^2 - 0.9419z + 0.381) (z^2 - 0.2782z + 0.2393) (z^2 - 1.126z + 0.7103)       

• (z-1.014), (z-1.01)

$$\frac{-4.6594(z+0.9096)(z-0.9577)(z-0.9488)(z-0.9313)(z-0.9179)(z-0.3913)(z^2-1.979z+0.9787)(z^2-2z+1)(z^2+2.457z+1.512)(z^2+1.252z+1.29)}{(z+0.9837)(z-0.9577)(z-0.989)(z-0.9179)(z-0.3926)(z^2-2z+1)(z^2-1.879z+0.8836)(z^2+1.509z+0.5897)(z^2+1.266z+0.6624)(z^2+0.1327z+0.6871)}$$ $$\frac{-4.659z^{10}-1.716z^9+15.31z^8+8.983z^7-16.5z^6-20.84z^5+7.966z^4+22.24z^3-5.169z^2-8.421z+2.797}{z^{11}+0.6308z^{10}-1.742z^9-1.756z^8+0.1252z^7+1.155z^6+1.153z^5+0.4067z^4-0.5311z^3-0.5307z^2-0.0004449z+0.09058}$$ $$\frac{-4.67z^7+6.56z^6-2.35z^5+0.25z^4-0.14z^3-0.45z^2-0.77z^1+0.44z^0}{z^8+-1.40z^7-0.86z^6-0.28z^5+0.077z^4-0.014z^3+0.005z^2+0.0045z^1-0.0037z^0}$$

>> realWPoles

realWPoles =

  -0.646350111691813  -0.604109913948706  -0.615540744061376   0.851185476739658  -0.018723272511901   0.586722340486274

>> complexWPoles

complexWPoles =

  Columns 1 through 3

 -0.624097753060113 + 0.068335354545306i -0.624097753060113 - 0.068335354545306i  0.692620579127527 + 0.148286121140251i

  Columns 4 through 6

  0.692620579127527 - 0.148286121140251i  0.961762578049797 + 0.051667985413578i  0.961762578049797 - 0.051667985413578i


DEN = 1	2.32391687368473	1.71748265453187	0.306523365158218	0.0973818300340791	0.362940480525279	0.257592593409259	0.0699629092830807	0.00711049156419029

NUM = 0	-4.64278912827070	-10.7381050821537	-7.92937212570451	1.40955870324541	7.03784669890844	6.16352223893136	3.09905279584263	0.834999628934847

Sharp and smooth:

realWPoles
0.685582047559997   0.886941632813173   0.453856743319766   0.364022455055491   0.279995573174802  -0.364552450892025   0.459650611494159

complexWPoles
0.514939968632107 + 0.027572970951922i  0.514939968632107 - 0.027572970951922i  0.925954904074920 + 0.182689904503936i
0.925954904074920 - 0.182689904503936i

a = [0	-4.63017013855327	-0.541121146334854	0.488939879951233	-0.0796591716695027	2.23719691145781	1.24998242888679]

b = [1	0.118235828497067	-0.136941582187522	0.315644536116788	0.121331278152849	0.0309302634227834	0.0124369244695385]

--- stepinfo results ---
Rise time:        0.8833 s
Settling time:    8.8005 s
Overshoot:        53.18 %
Peak value:       0.229770
Peak time:        2.9250 s (relative to step)
Max absolute control input (outer loop): 0.705913

Small and smooth:

complexWPoles =

  Columns 1 through 3

  0.962238972941220 + 0.160853867173318i  0.962238972941220 - 0.160853867173318i  0.780908963708176 + 0.070665381901577i

  Columns 4 through 6

  0.780908963708176 - 0.070665381901577i -0.042557536614824 + 0.272270171620581i -0.042557536614824 - 0.272270171620581i

  Columns 7 through 9

  0.324214160145899 + 0.130726288120701i  0.324214160145899 - 0.130726288120701i  0.700897388099629 + 0.118810586847621i

  Columns 10 through 12

  0.700897388099629 - 0.118810586847621i -0.062161956006528 + 0.134999746092694i -0.062161956006528 - 0.134999746092694i

--- stepinfo results ---
Rise time:        1.0260 s
Settling time:    6.6956 s
Overshoot:        52.97 %
Peak value:       0.229452
Peak time:        3.4000 s (relative to step)
Max absolute control input (outer loop): 0.707785

a = 0	-4.66666666666561	6.55807404548921	-2.35152184569356	0.252001685598733	-0.140587327293981	0.448927352425222	-0.765490360821796	0.446220137102285

b = 1	-1.40250276213874	0.863588307968022	-0.275523174073078	0.0770775517460313	-0.0139612597512338	0.00533288818588099	0.00449790914409875	0.00366435670305026

Idek:

a = 0	-4.66666657112297	-5.71334467533668	0.527758031044943	3.63303268343666	2.04550237640322	1.18581671921380	0.782906356262210

b = 1	1.24801406332115	0.294056019090973	-0.0973944976857719	0.0817110767707347	0.0998188345074395	0.0260650996452369	0.00167589286850688

--- stepinfo results ---
Rise time:        1.0299 s
Settling time:    6.7485 s
Overshoot:        52.89 %
Peak value:       0.229329
Peak time:        3.3750 s (relative to step)

complexWPoles =

  Columns 1 through 3

  0.202682008587372 + 0.218692740238697i  0.202682008587372 - 0.218692740238697i  0.780842555624275 + 0.108551754063571i

  Columns 4 through 6

  0.780842555624275 - 0.108551754063571i -0.586695522067549 + 0.159084324199343i -0.586695522067549 - 0.159084324199343i

  Columns 7 through 9

  0.845862338391385 + 0.062984648555661i  0.845862338391385 - 0.062984648555661i  0.954396500118466 + 0.124909153605916i

  Columns 10 through 12

  0.954396500118466 - 0.124909153605916i -0.458046376414991 + 0.219221779306105i -0.458046376414991 - 0.219221779306105i

premature ejaculator:

a = 0 -4.66666666612145 -2.53001626261064 6.40237628863966 3.80858929784358 4.99671880250496 3.03559201542027 -10.7623268428793 -7.61777537027848 4.04655017448160 3.27205316579321

b = 1 0.542136240587238 -1.40969546526838 -0.829705229476998 0.378821781406049 0.159470060848469 -0.136988979351436 0.0251118109414924 0.166401276848355 0.114283362297186 0.0267442455030135

realWPoles =   Columns 1 through 7

  -0.355486999903681  -0.226089137169729   0.449032849681427   0.925162789669499   0.931069494432920   0.250460767690531   0.696148595728408

  Columns 8 through 12

  -0.418224746922088  -0.242728000905881  -0.533935764778620   0.958036544793448  -0.975587316687368

--- stepinfo results ---
Rise time:        0.8728 s
Settling time:    5.8349 s
Overshoot:        43.71 %
Peak value:       0.217129
Peak time:        2.9000 s (relative to step)
Max absolute control input (outer loop): 0.707785

the final contender (resembles mr. smooth)

realWPoles =

   0.980818186081497  -0.657805375303224   0.010427808533015  -0.179445368936604


complexWPoles =

  Columns 1 through 3

  0.867623228879922 + 0.147471886104563i  0.867623228879922 - 0.147471886104563i  0.401340715904988 + 0.109104534411110i

  Columns 4 through 6

  0.401340715904988 - 0.109104534411110i -0.297530306009091 + 0.280939647977631i -0.297530306009091 - 0.280939647977631i

  Columns 7 through 8

  0.444482233059823 + 0.248682541974162i  0.444482233059823 - 0.248682541974162i

a = 0 -3.96656697517943 4.89789814578035 0.929615063808888 -2.51285436812469 0.337754867023365 0.372214611369375 -0.0127068495018990 0.150495930656101 0.139177275889914 -0.357738753446430

  
b = 1 -0.988263601992751 -0.281171863000745 0.495060802177993 -0.0565874582745965 -0.0790715161955462 -0.0172734978227051 0.00504036690743160 -0.0109291444288046 -0.00821470872316814 -0.00287859617870927

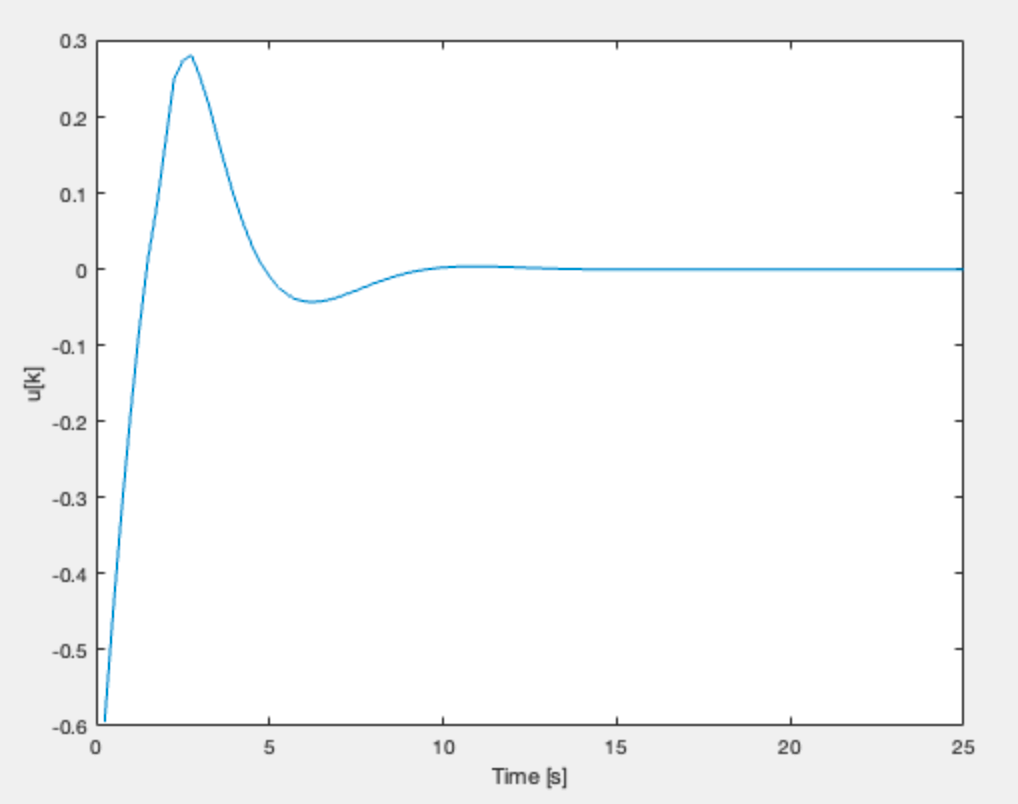
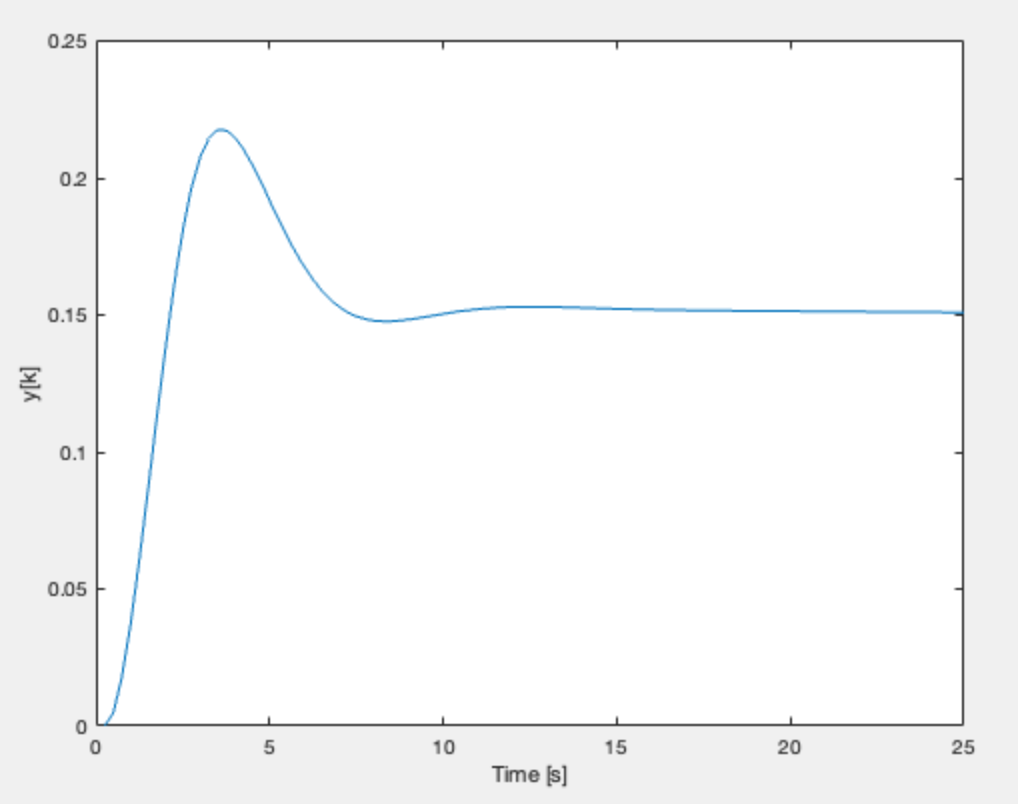
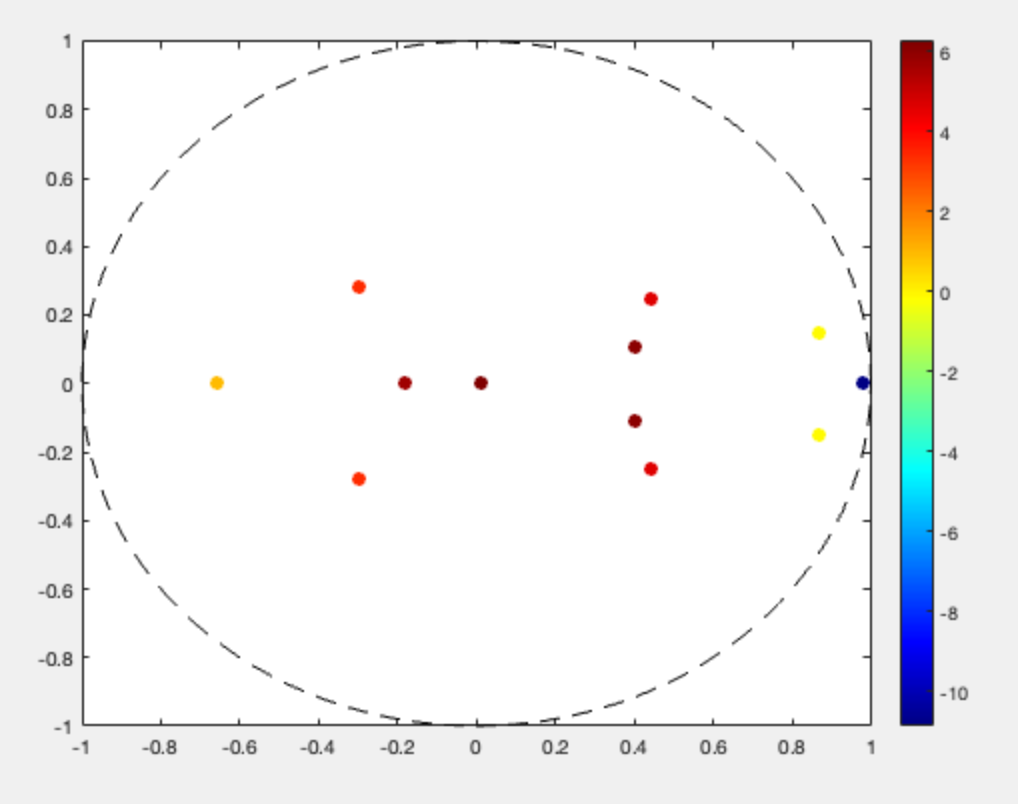
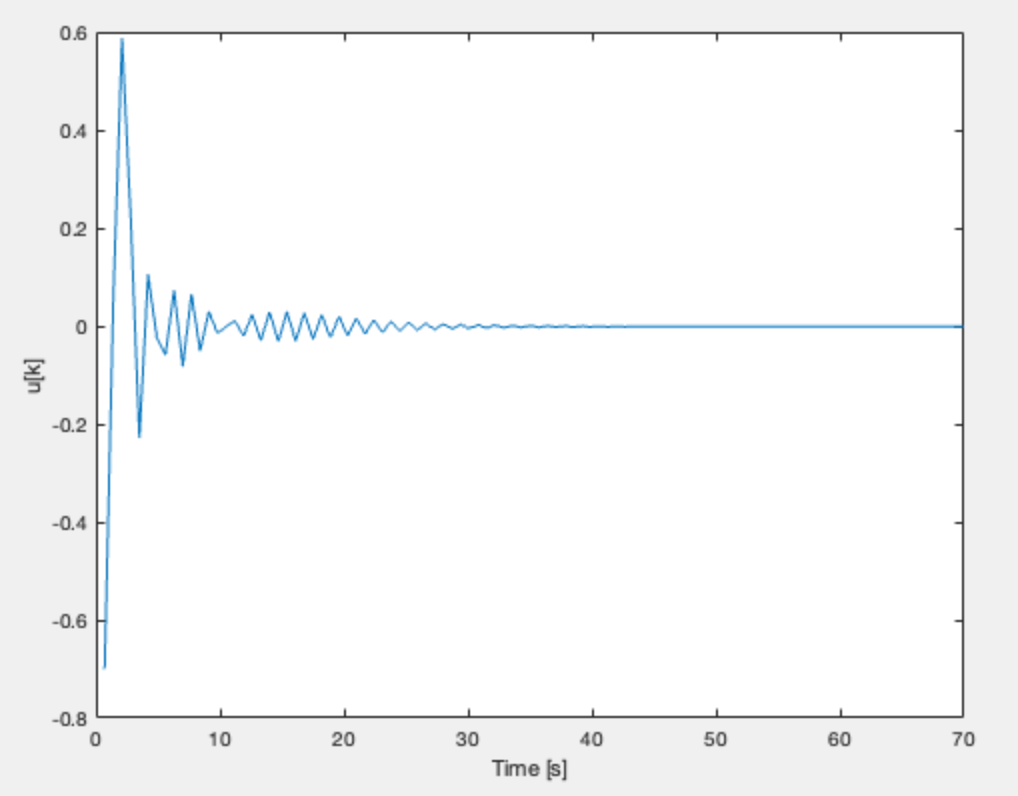
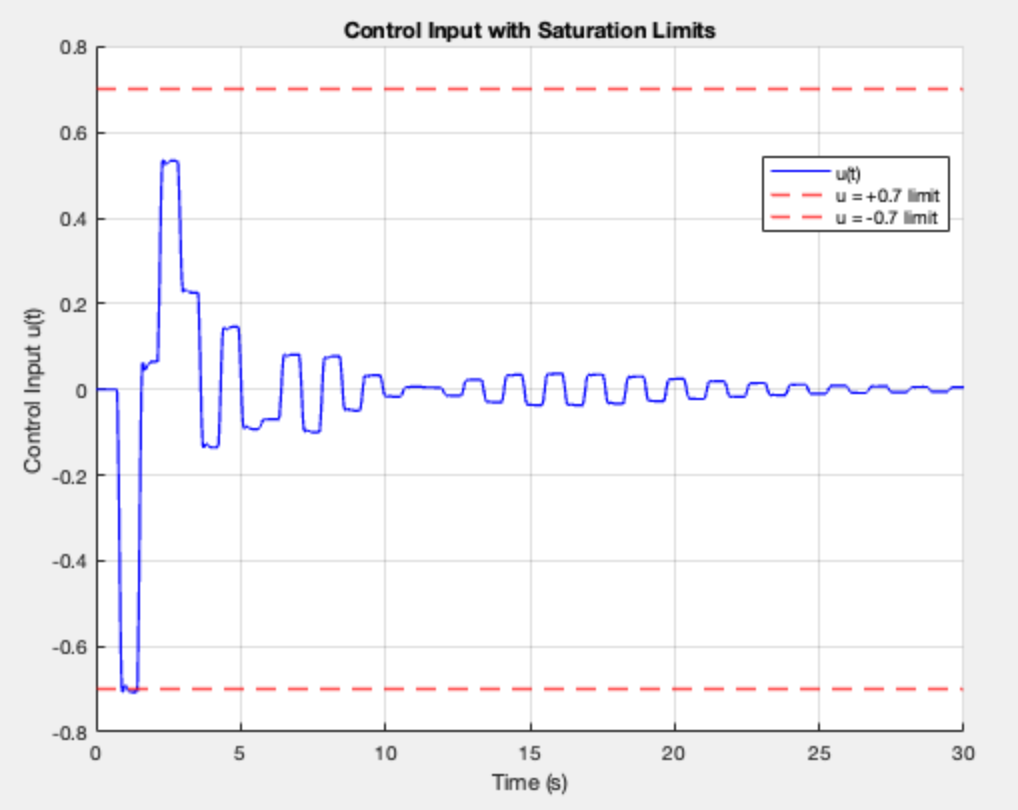
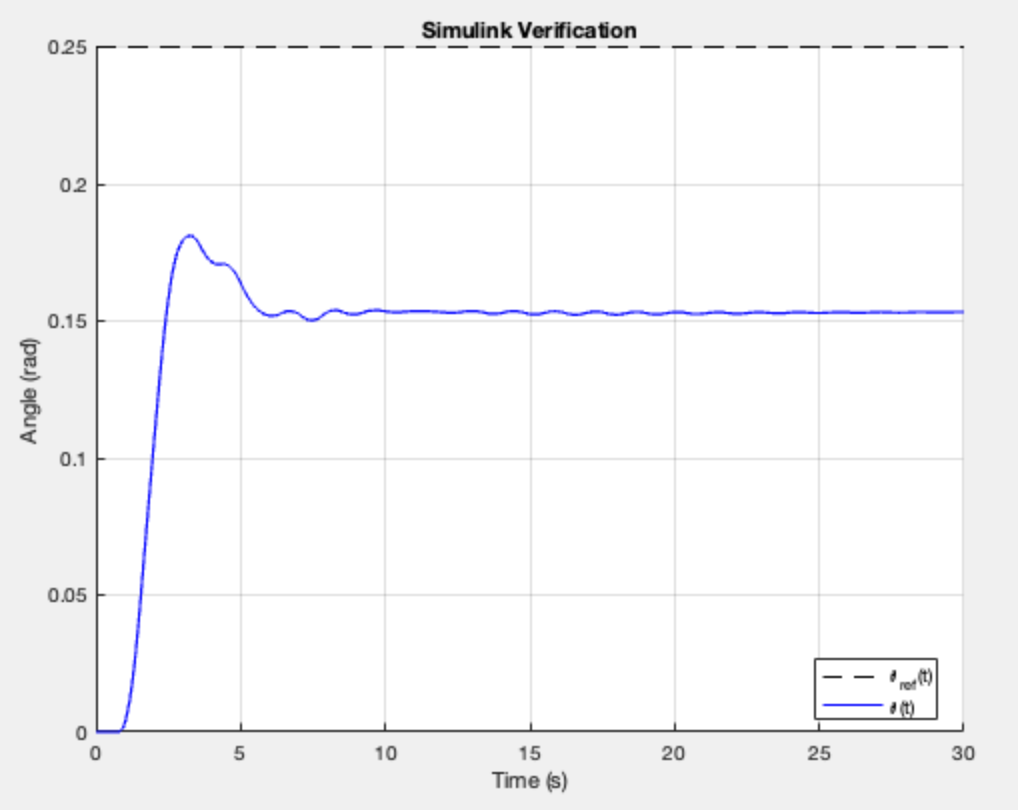
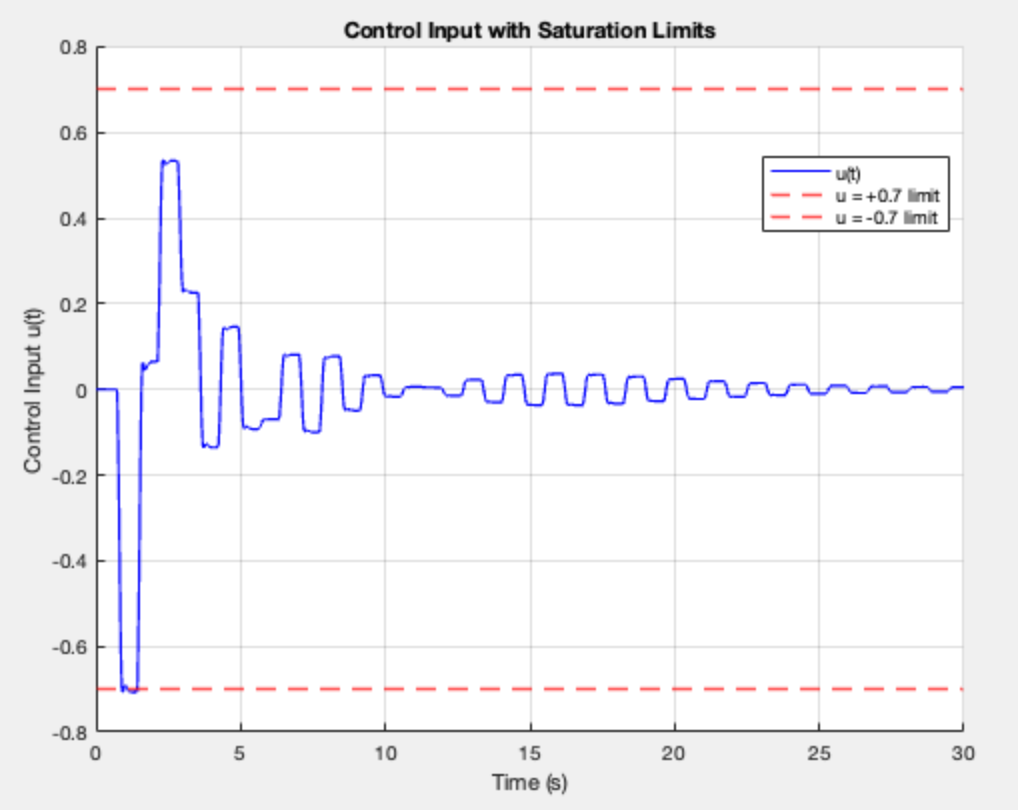
FAST and SHORT 0.7:

complexWPoles =

  Columns 1 through 3

  0.816203203434429 + 0.008671112907435i  0.816203203434429 - 0.008671112907435i -0.084606898110519 + 0.127490158804354i

  Column 4

 -0.084606898110519 - 0.127490158804354i

realWPoles =

  Columns 1 through 7

  -0.882091021381663   0.986832036535385  -0.614203034093135  -0.457400570606226  -0.774228116367801   0.891925124519857   0.311773117390400

  Column 8

   0.746255966896023

699 310