Discrete-Time Stability

An example discrete system:

$$\begin{array}{rl}x[k+1]& =\lambda x[k],\lambda \in \mathbb{C}\\ x^{+}& =\lambda x\end{array}$$

We can look at the behavior for various $\lambda$:

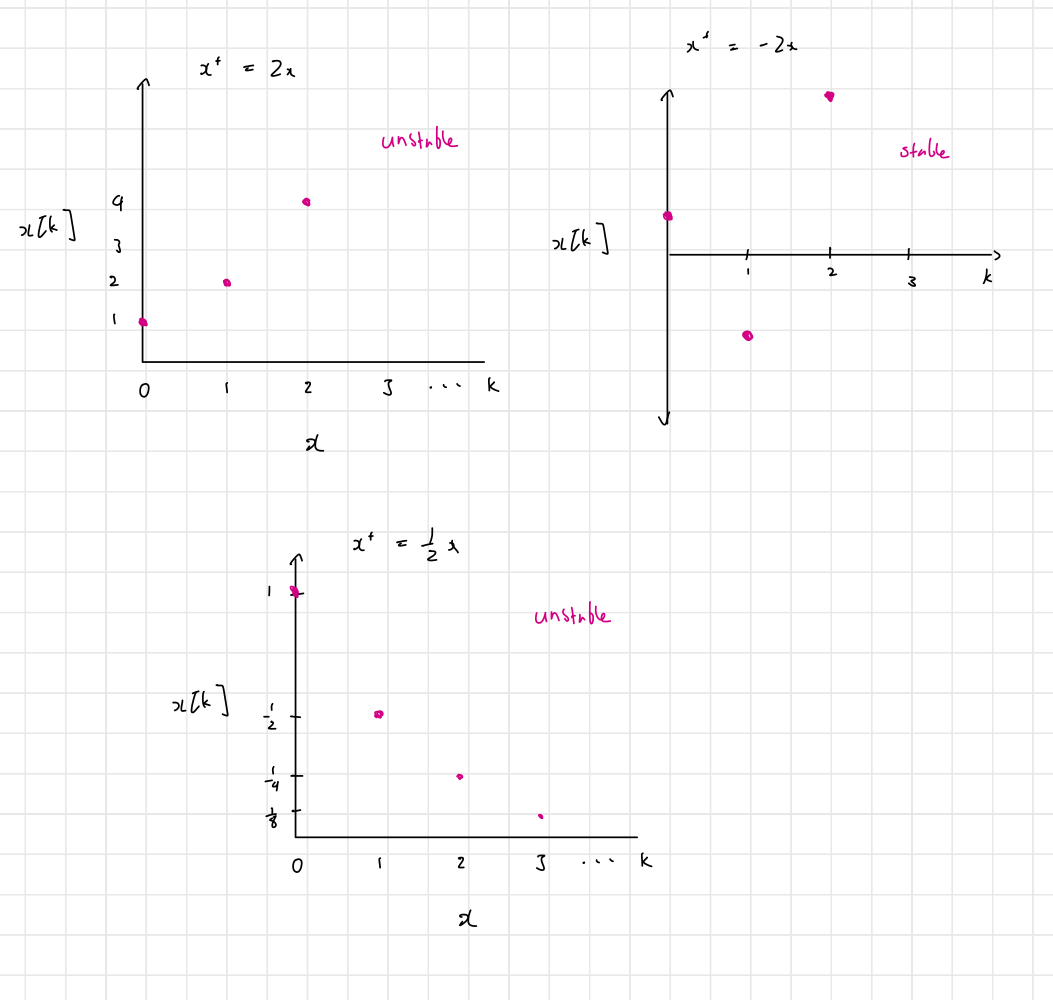
This behaves quite differently from a continuous-time system, motivating a different definition.

Looking at our system again:

$$\begin{array}{rl}{x}^{+}& =\lambda x\\ x[k]& =\lambda x[k-1]=\lambda (\lambda x[k-2])={\lambda }^{2}x[k-2]=\cdots ={\lambda }^{k}x[0]\\ x[k]& ={\lambda }^{k}x[0]\\ |x[k]|& =|\lambda {|}^k|x[0]|\end{array}$$

• Case 1: $|\lambda |<1$ – stable
• Case 2: $|\lambda |>1$ – unstable
• Case 3: $|\lambda |=1$ – unstable

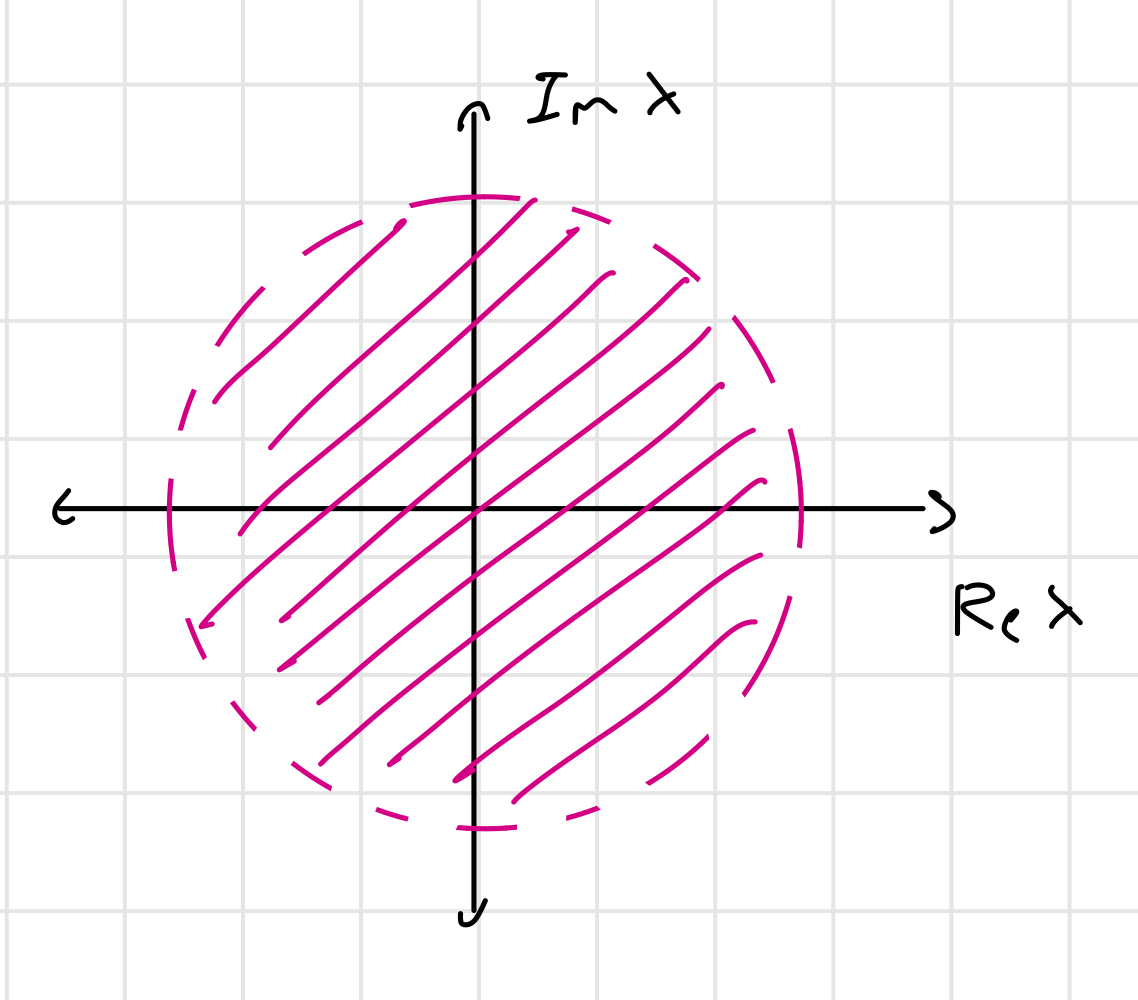
Thus, the region of stability for the discrete case is the open unit disk ($\mathbb{D}$):

Another example:

$$x^{+}=\lambda x+u$$

Taking the z-transform to move into the frequency domain:

$$zX[z]=\lambda X[z]+U[z]$$

• The time shift $x^{+}$ becomes a $z$

Solving for $X[z]$ gives:

$$X[z]=\frac{1}{z-\lambda }U[z]$$

Thus, $\lambda$ is a pole of this system.

Stability criterion for discrete-time systems

A real, rational, transfer function for a discrete-time $G[z]$ is stable if all all poles of $G[z]$ lie in $\mathbb{D}$.

Quick Examples

• $\frac{1}{z}$ is stable ($z=0$ is inside open unit disk)
• $\frac{1}{z+5}$ is unstable
• $\frac{1}{z-\frac{1}{2}}$ is stable
• $\frac{1}{z+1}$ is unstable (lies on border of open unit disk)