Force Analysis of Crank-Slider Linkage

For a crank-slider linkage, the problem set-up first requires that we know:

Angular and linear accelerations (determined through kinematic analysis)
Masses of links
Position information (link lengths, link positions, location of center of gravity for each link)
Mass moment of inertia with respect to CG, $I_{G}$ , for each link

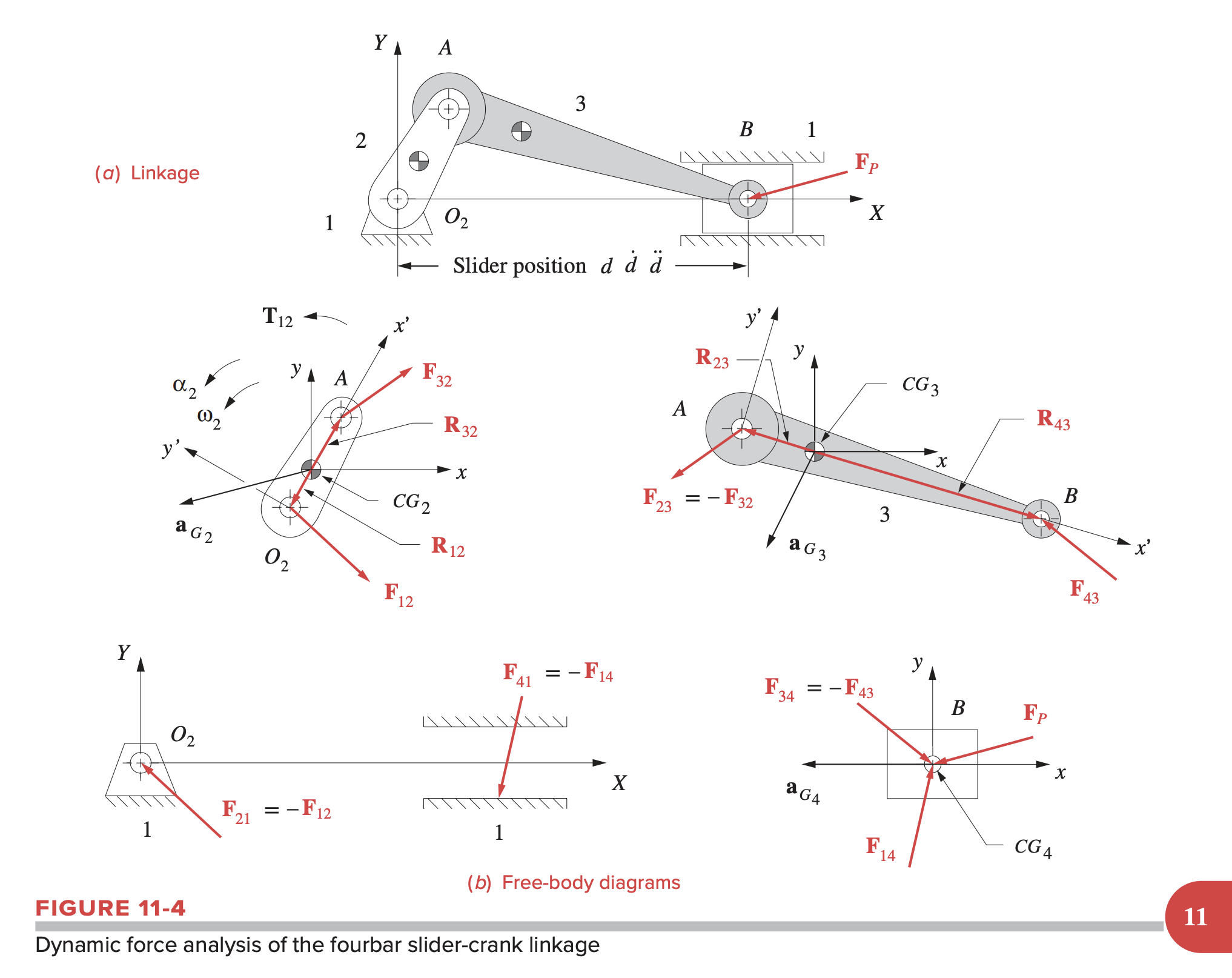
We then write out the forces and moments for each link.

Link 2:

F_{12 x} F_{12 y} T_{12} + F_{32 x} = m_{2} a_{G_{2 x}} + F_{32 y} = m_{2} a_{G_{2 y}} + (R_{12 x} F_{12 y} - R_{12 y} F_{12 x}) + (R_{32 x} F_{12 y} - R_{32 y} F_{32 x}) = I_{G_{2}} α_{2}

Link 3:

F_{43 x} F_{12 y} (R_{43 x} - F_{32 x} = m_{3} a_{G_{3 x}} - F_{32 y} = m_{3} a_{G_{3 y}} F_{43 y} - R_{43 y} F_{43 x}) + (R_{23 x} F_{32 y} - R_{23 y} F_{32 x}) = I_{G_{3}} α_{3}

Link 4:

F_{14 x} - F_{14 y} - (R_{14 x} F_{43 x} + F_{P x} = m_{4} a_{G_{4 x}} F_{43 y} + F_{P y} = m_{4} a_{G_{4 y}} F_{14 y} - R_{14 y} F_{14 x}) - (R_{34 x} F_{43 y} - R_{34 y} F_{43 x}) + (R_{P x} F_{P y} - R_{P y} F_{P x}) = I_{G_{4}} α_{4}

Considering that we have a crank-slider means:

α_{4} = 0, a_{G_{4 y}} = 0

We need to consider the friction force $f$ at the interface:

f = \pm μ N

Signs will be opposite of slider velocity, $\dot{d}$ .

Examining friction force:

F_{14 x} = - μ SGN (\dot{d}) ∣ F_{14 y} ∣

where the $SGN$ function returns the sign of $\dot{d}$ .

Considering acceleration specifics regarding Link 4 and friction force, the Link 4 equations become:

- μ SGN (\dot{d}) ∣ F_{14 y} ∣ - F_{14 y} - F_{43 x} + F_{P x} = m_{4} a_{G_{4 x}} F_{43 y} + F_{P y} = m_{4} a_{G_{4 y}}

This finally gives us a system with 8 unknowns:

10 - R_{12 y} 00000 01 R_{12 x} 00000 10 - R_{32 y} - 1 0 R_{23 y} 00 01 R_{32 x} 0 - 1 - R_{23 x} 00 00010 - R_{43 y} - 1 0 00001 R_{43 x} 0 - 1 000000 μ SGN (\dot{d}) 1 00100000 F_{12 x} F_{12 y} F_{32 x} F_{32 y} F_{43 x} F_{43 y} F_{14 y} T_{12} = m_{2} a_{G_{2 x}} m_{2} a_{G_{2 y}} I_{G_{2}} α_{2} m_{3} a_{G_{3 x}} m_{3} a_{G_{3 y}} I_{G_{3}} α_{3} m_{4} a_{G_{4 x}} - F_{P x} - F_{P y}

[A] [B] = [C]

We can then take the inverse of the matrix to solve:

[B] = [A]^{- 1} [C]

/notes/