Finite Element Method

The Finite Element Method (FEM) is a method for solving partial differential equations and operates around discretizing the domain into simply shaped sub-regions or “elements”. An approximate solution to the PDE can be developed for each element, and then the total solution is generated by linking together (assembling) the elements. By enforcing continuity at the element boundaries, we can create a system of equations.

Some notes:

• The elements can vary in shape so that we can represent complex geometry.
• The elements allow us to predict values across the entire solution domain, rather than at discrete points (FDM).
• The accuracy of the method depends on the the quality of element shapes and the size of the elements.

Step 1: Discretize

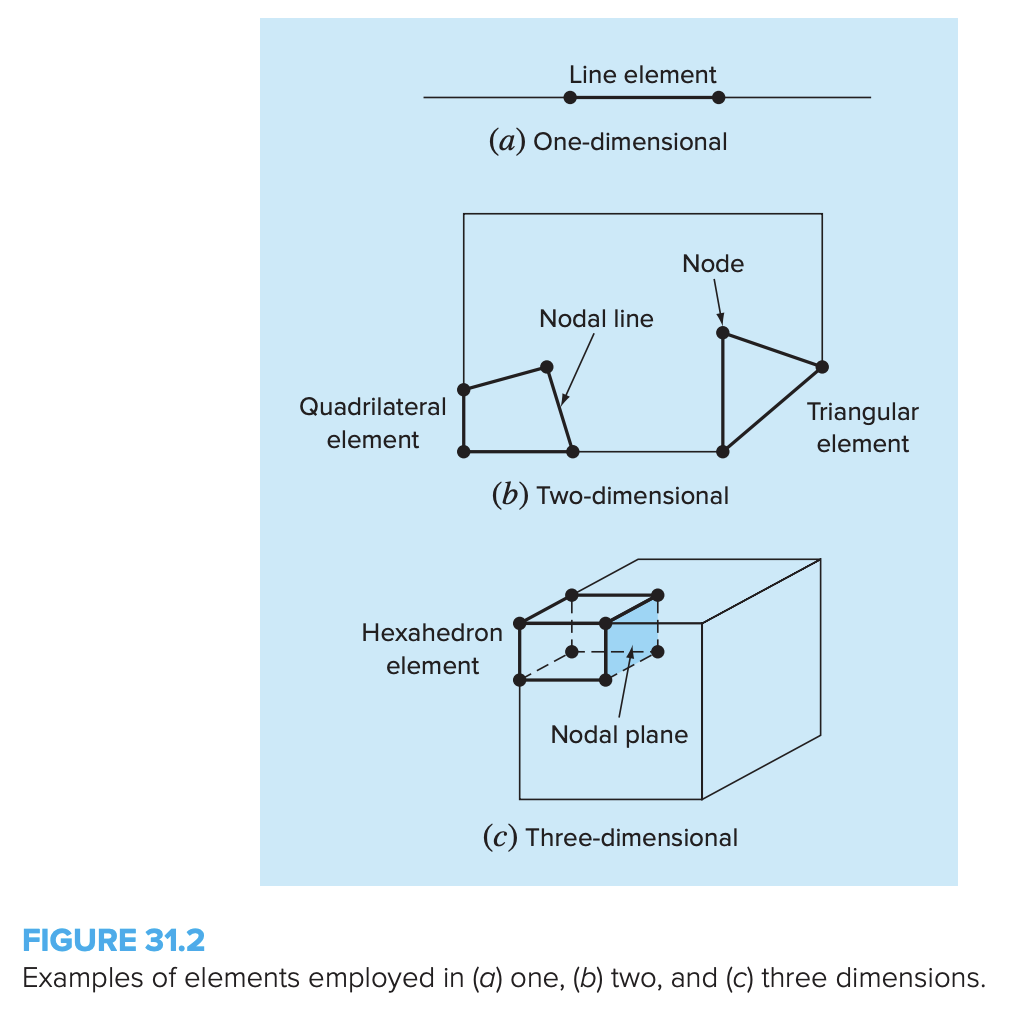
We need to first discretize the solution domain into elements.

• Nodes: Points in space with $(x,y,z)$ coordinates.
• Elements: Define the connectivity of nodes to form a link (1D), enclosed area (2D) or enclosed volume (3D).

Step 2: Develop element equations

First:

1. Identify a function with (unknown) coefficients to approximate the solution within the element.
2. Evaluate the coefficient so that the function approximates the solution.

Polynomials are often used for convenience. To start, consider a first-order polynomial (straight line):

$$u(x)=a_0+a_{1}x$$

To enforce continuity, the function needs to pass through the values $u(x)$ at the endpoints of the element ($x_1$ and $x_2$).

$$\begin{array}{r}{u}_1=a_0+a_1{x}_1\\ u_2=a_0+a_1{x}_2\end{array}$$

Using Cramer’s Rule, we have:

$$a_0=\frac{u_1{x}_2-u_2{x}_1}{x_2-x_1},a_1=\frac{u_2-u_1}{x_2-x_1}$$

We can write this as:

$$u=N_1{u}_1+N_2{u}_2$$

where $N_1=\frac{x_2-x}{x_2-x_1},N_2=\frac{x-x_1}{x_2-x_1}$, where $N_1,N_2$ are the interpolation functions.

Note that we can both differentiate and integrate the shape function.

$$\begin{array}{rl}\frac{du}{dx}& =\frac{1}{x_2-x_1}(-u_1+u_2)\\ {\int }_{x_1}^{x_2}udx& =\frac{u_1+u_2}{2}(x_2-x_1)\end{array}$$

Step 3: Develop element equations based on ODE or PDE

Specific to the function. Develop element equations based on the ODE or PDE

• Method of Weighted Residuals (MWR)

Step 4: Assembly of elements into system of equations

Step 5: Apply boundary conditions (BC’s)

Step 6: Solve system of equations