Bayesian Inference

The maximum likelihood criterion approach to learning is generally overconfident; it selects the most likely parameters during training and uses these to make predictions. However, many parameter values may be broadly compatible with the data and only slightly less likely. The Bayesian approach treats the parameters as unknown variables and computes a distribution $Pr(\varphi |\{{\mathbf{x}}_i,{\mathbf{y}}_i\})$ over the parameters $\varphi$, conditioned on the training data $\{{\mathbf{x}}_i,{\mathbf{y}}_i\}$, using Bayes’ Rule:

$$Pr(\varphi |\{{\mathbf{x}}_i,{\mathbf{y}}_i\})=\frac{{\prod }_{i=1}^{I}Pr({\mathbf{y}}_{\mathbf{i}}|{\mathbf{x}}_{\mathbf{i}},\varphi )Pr(\varphi )}{\int {\prod }_{i=1}^{I}Pr({\mathbf{y}}_{\mathbf{i}}|{\mathbf{x}}_{\mathbf{i}},\varphi )Pr(\varphi )d\varphi }$$

where $Pr(\varphi )$ is the prior probability of the parameters, and the denominator is a normalizing term. Hence, very parameter choice is assigned a probability.

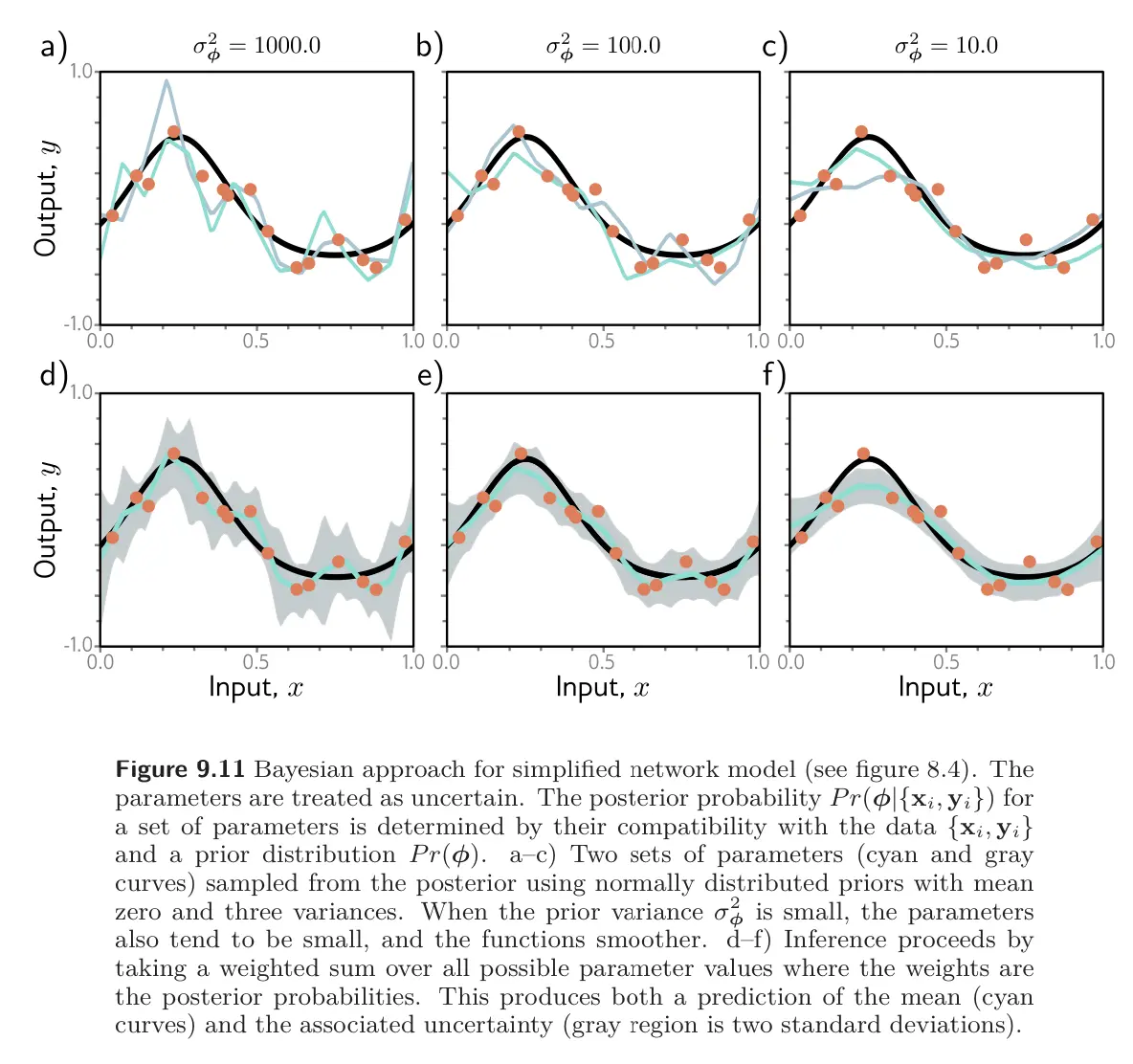
The prediction $\mathbf{y}$ for new input $\mathbf{x}$ is an infinite weighted sum (an integral) of the predictions for each parameter set, where the weights are the associated probabilities:

$$Pr(\mathbf{y}|\mathbf{x},\{{\mathbf{x}}_i,{\mathbf{y}}_i\})=\int Pr(\mathbf{y}|\mathbf{x},\varphi )Pr(\varphi |\{{\mathbf{x}}_i,{\mathbf{y}}_i\})d\varphi$$

This is effectively an infinite weighted ensemble, where the weight depends on (i) the prior probability of the parameters and (ii) their agreement with the data.

The Bayesian approach is elegant and can provide more robust predictions than those that derive from maximum likelihood. Unfortunately, for complex models like neural networks, there is no way to represent the full probability distribution over the parameters or integrate over it during inference. Thus, all current methods of this type must make an approximation of some kind, addying considerably complexity to learning and inference.