Iterative Deepening Search

Iterative deepening search runs depth-limited search with gradually increasing depth ($\ell =0,1,2,3,\dots$).

This aims to combine the space efficiency of DFS with BFS completeness. This re-expands nodes, but the cost is generally acceptable.

Properties:

• Complete: Yes (assuming finite branching)
• Optimal: Yes (assuming unit step costs)
• Time: $O(b^d)$
• Space: $O(bd)$

We can see that this has the same asymptotic time as BFS, with space usage like DFS.

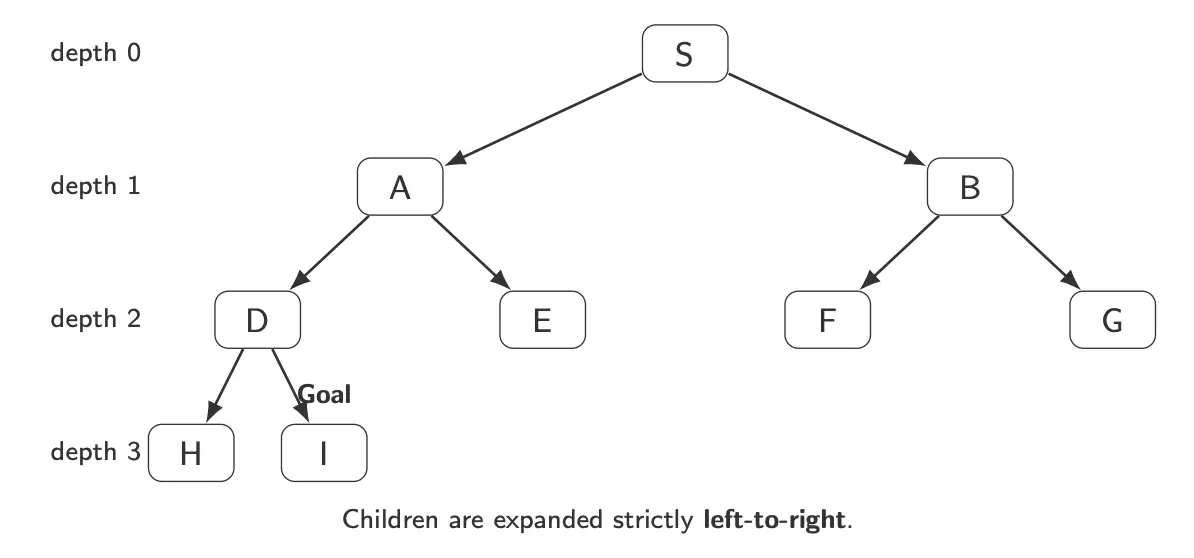
Why is IDS still worth it even with re-expansion? Consider the number of nodes expanded per iteration for the example above:

$$\begin{array}{r}N(0)=1\\ N(1)=3\\ N(2)=7\\ N(3)=5\end{array}$$

Thus, the total expansions performed by IDS until the goal is $1+3+7+5=16$. The number of unique nodes explored is $\{S,A,B,D,E,F,G,H,I\}⟹9$.

Thus, most re-expansion is done near the top of the tree (small depth), which is cheap. As depth grows, the number of nodes at depth $d$ dominates anyway. Furthermore, IDS keeps space like DFS ($O(bd)$), not $O(b^d)$ like BFS.