In game playing as search, there is an opponent, unlike classical search. The objective is not only to find the best
Given a board configuration, we search for the best move. The opponent responds with a move, producing a new board. Then, we search again from the new configuration. Note that time is limited for each search, and most game positions are non-terminal (termination may occur far beyond the search horizon).
Problem Formulation
Initial state:
- Initial board configuration
- Player to move
Operators:
- Legal moves available to the current player
Utility (payoff) function:
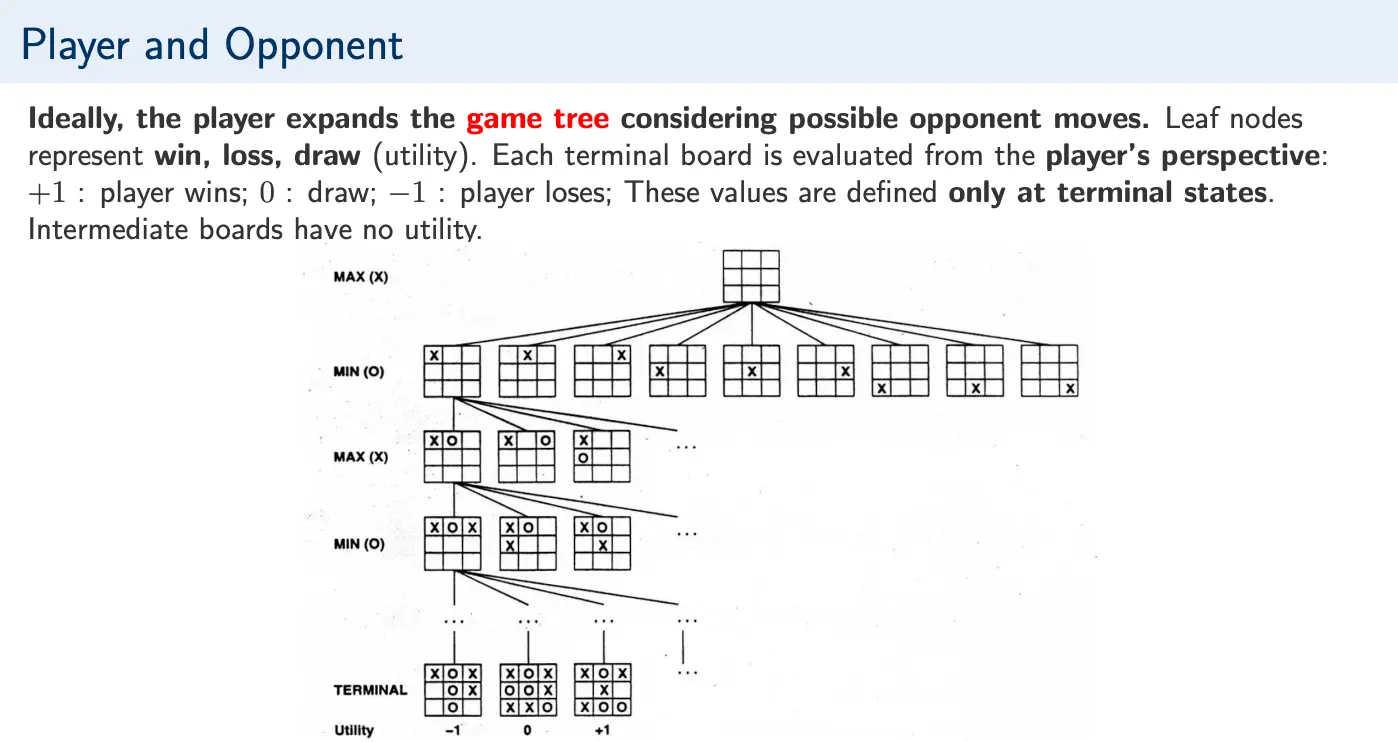
- A function that assigns a numerical value to a terminal game state, representing the outcome of the game from the perspective of a player.
The search objective is then to find a sequence of moves that maximizes the player’s utility, explicitly accounting for the opponent’s moves. Generally, we assume that the opponent is rational and tries to optimize their own utility.
Types of Games
Perfect information games:
- Each player has complete information about opponent’s position and available actions
- Deterministic examples: Chess, checkers
- With chance: Backgammon, Monopoly
Imperfect information games:
- Players do not have complete information about opponent’s position and available actions
- Typically involve chance: Poker, bridge