Alpha-Beta Pruning

Algorithms Explained – minimax and alpha-beta pruning

In adversarial search, many branches are irrelevant. If the position is already not better than what we can get elsewhere, it is not worth exploring further. If the opponent can force a bad outcome, exploring good replies that the opponent will never allow is wasted work. So, we can prune subtrees that cannot affect the minimax decision.

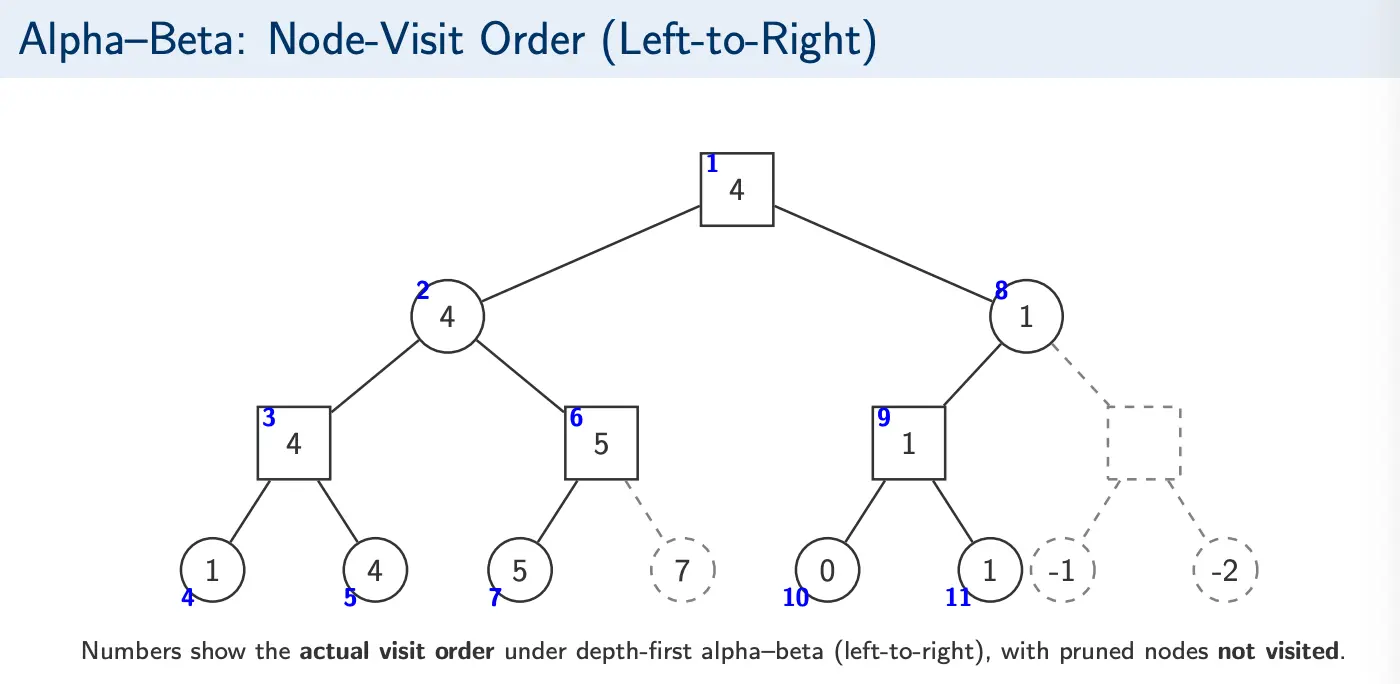
Minimax explores about $O(b^d)$ nodes, alpha-beta return the same minimax decision, but prunes branches that cannot affect the backed-up value. With good move ordering, the effective branching factor drops such that $b_{\text{eff}}\ll b$. In the best case:

$$N_{\alpha \beta }(d)\approx O(b^{d/2})⟹b_{\text{eff}}\approx \sqrt{b}$$

Alpha and Beta Bounds

$\alpha$:

• Best (highest) value found so far for MAX
• Lower bound on what MAX can guarantee
• Increasing (non-decreasing) along a path

$\beta$:

• Best (lowest) value found so far MIN
• Upper bound on what MIN can force
• Decreasing (non-increasing) along a path

Algorithm

1. Perform depth-first minimax search.
2. Maintain bounds $(\alpha ,\beta )$ along each path. Start at $\alpha =-\infty ,\beta =+\infty$.
3. At MAX nodes:
   • Update $\alpha =\max (\alpha ,v)$
   • Prune if $\alpha \ge \beta$
4. At MIN nodes:
   • Update $\beta =\min (\beta ,v)$
   • Prune if $\beta \le \alpha$

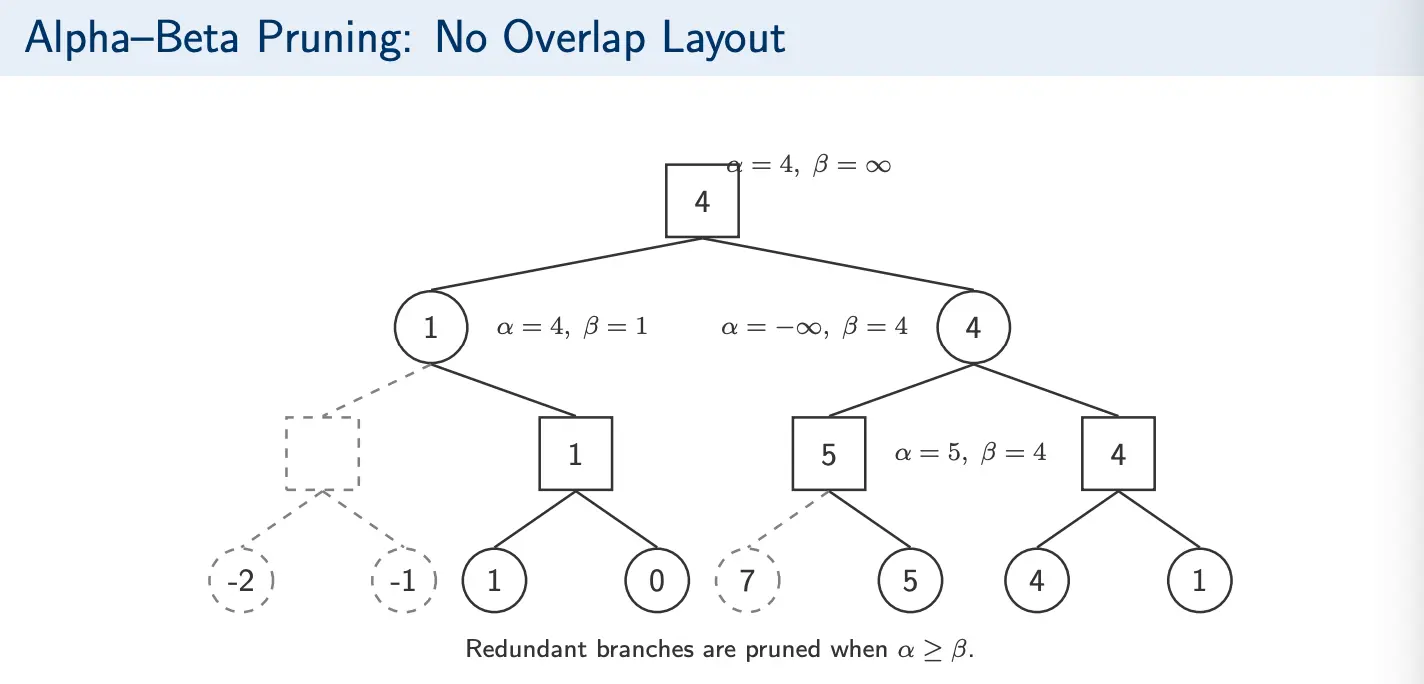
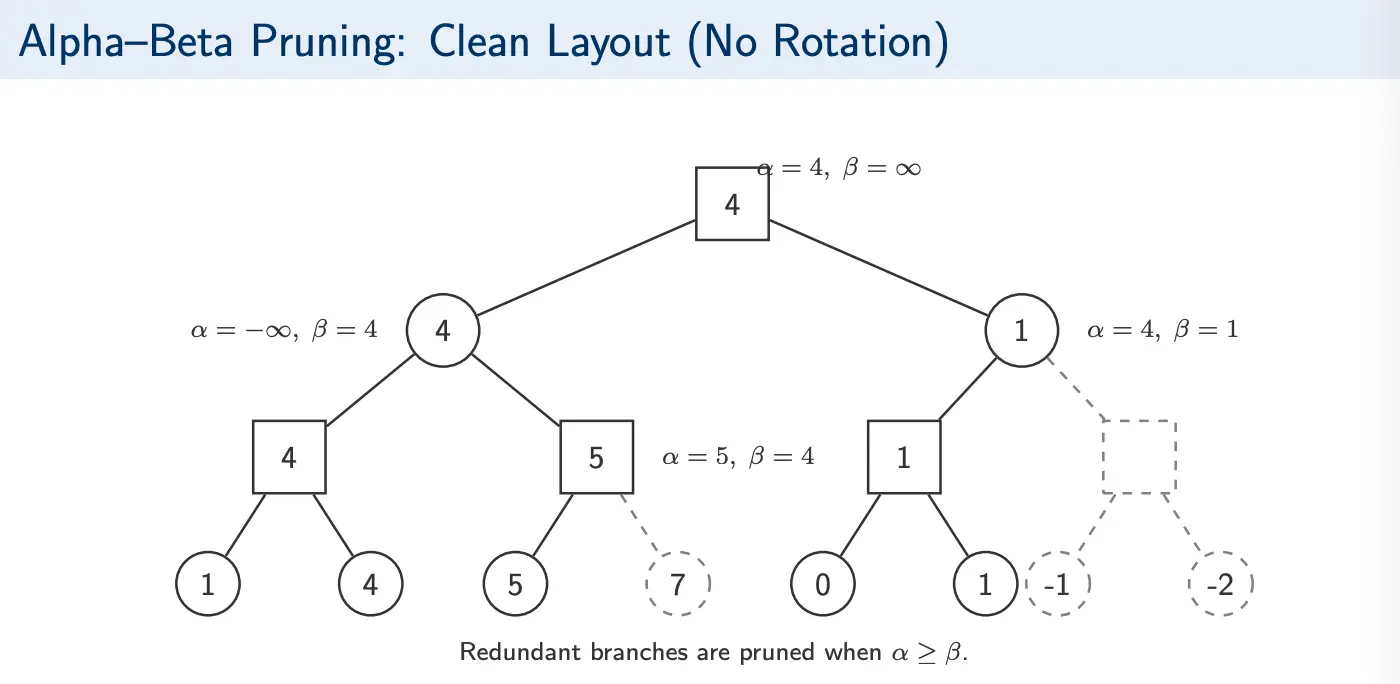
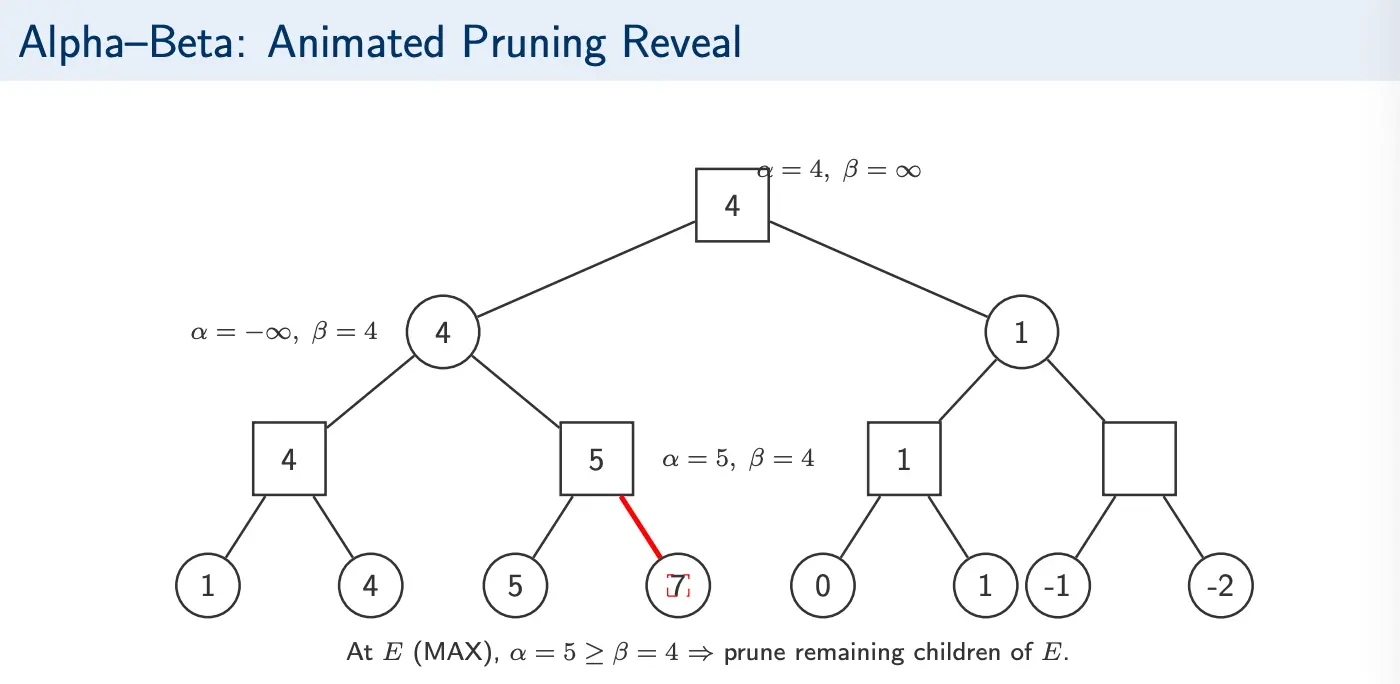
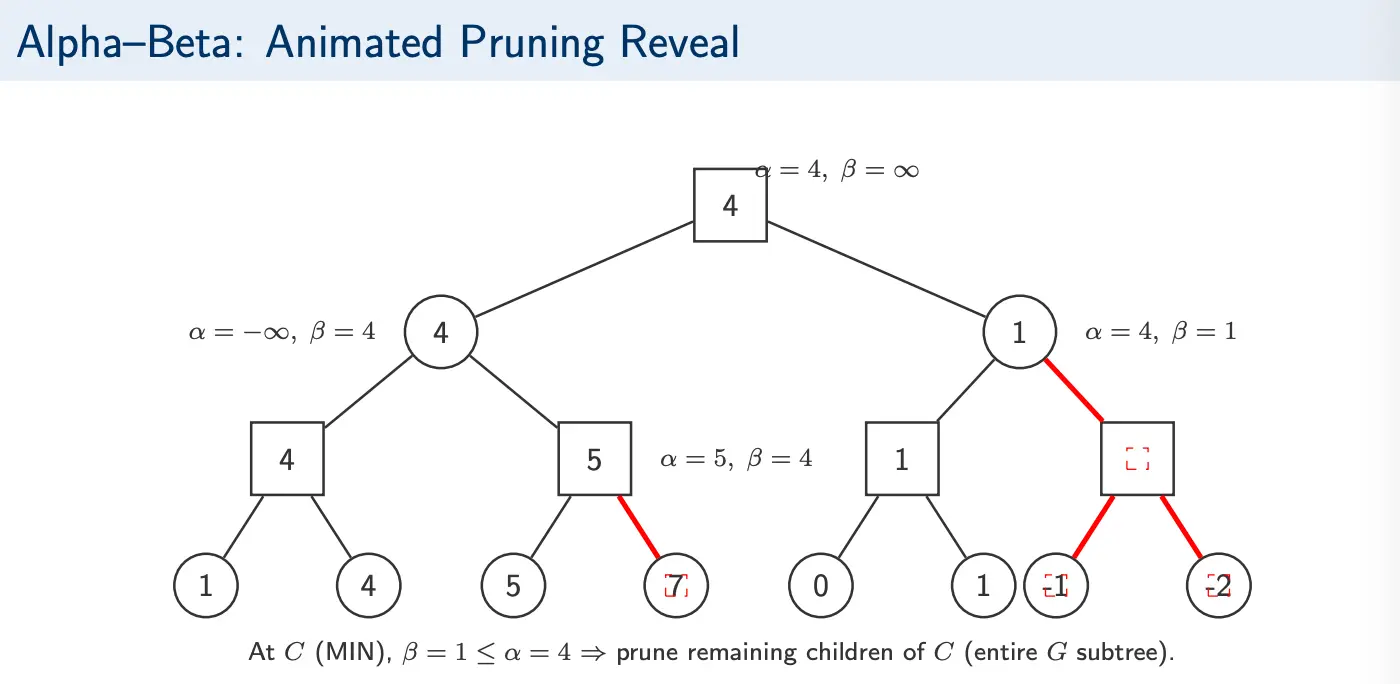
Alpha cutoff: While exploring a MIN node, if the current best values $v$ satisfies $v\le \alpha$, then MAX already has an alternative guaranteeing at least $\alpha$. So MIN will never choose this branch, and we will prune the remaining children.

Beta cutoff: While exploring a MAX node, if the current best value $v$ satisfies $v\ge \beta$, then MIN already has an alternative limiting MAX to at most $\beta$. So, this branch cannot improve the outcome and the remaining children will be pruned.

Properties

• Complete: Yes (for finite game trees).
• Optimal: Yes (against an optimal opponent).
• Worst-case time: $O(b^d)$ (same as minimax).
• Best-case time: $O(b^{d/2})$ with perfect move ordering.
• Space complexity: $O(bd)$ using depth-first search.

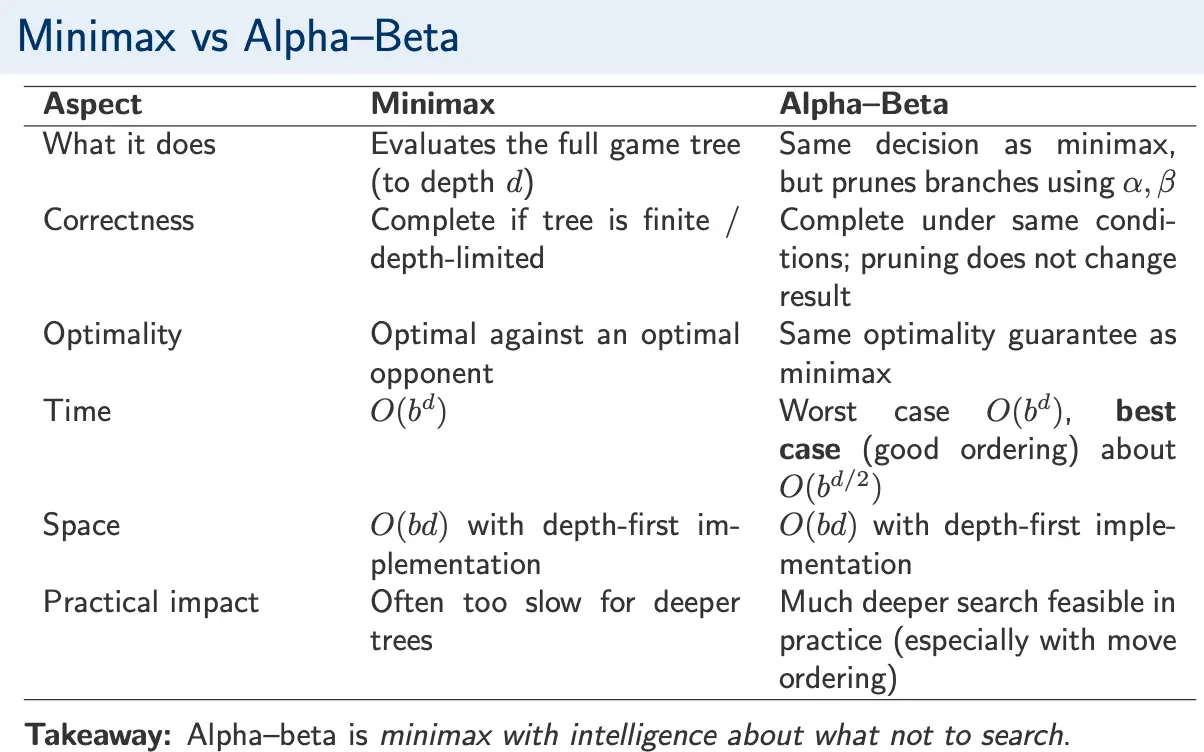
Comparison to Minimax

Alpha-beta returns the same optimal move/value, but fewer nodes are evaluated with pruning. However, the savings strongly depend on move ordering.

If good moves are explored first, $\alpha$ rises quickly at MAX nodes and $\beta$ drops quickly at MIN nodes. Many siblings satisfy $\alpha \ge \beta$ early. In the worst case, where bad moves are explored first, the bounds tighten slowly, with few/no cutoffs.

Thus, move-ordering heuristics are often used to sort children using a score that can be calculated quickly. Then we sort using the score, descending at MAX and ascending at MIN.

Examples

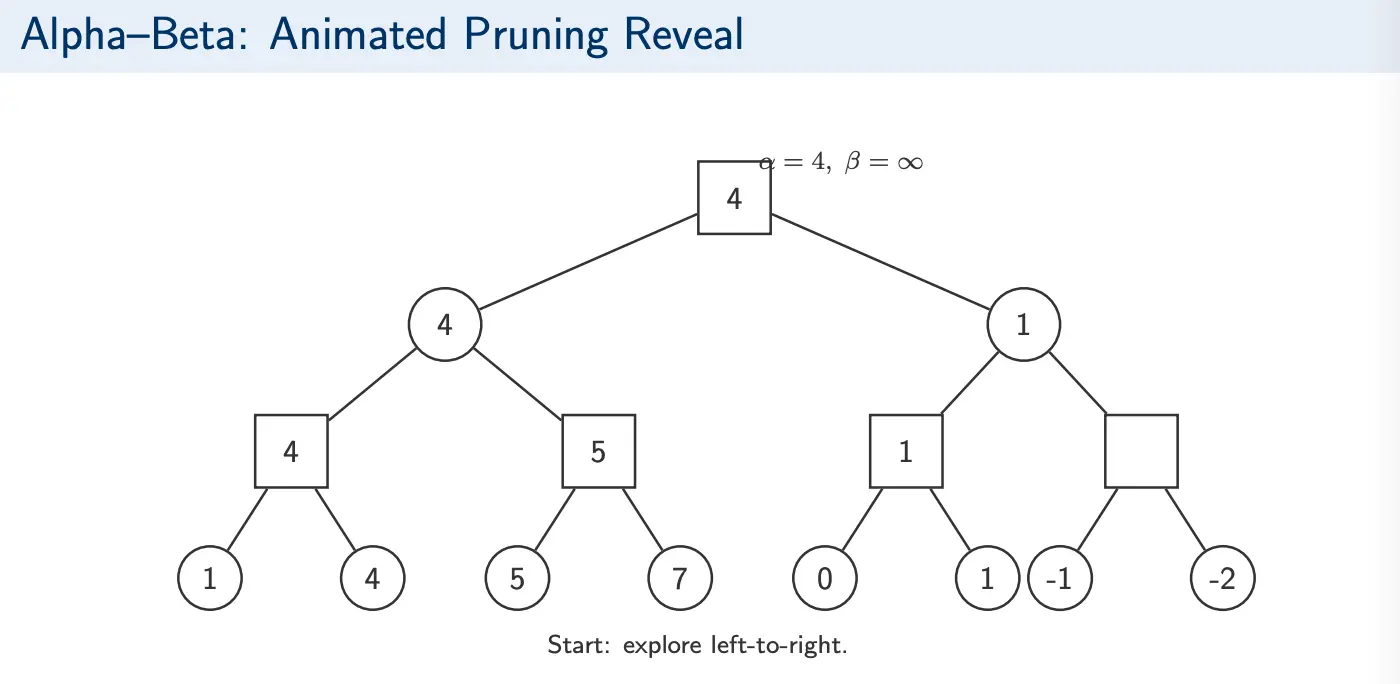
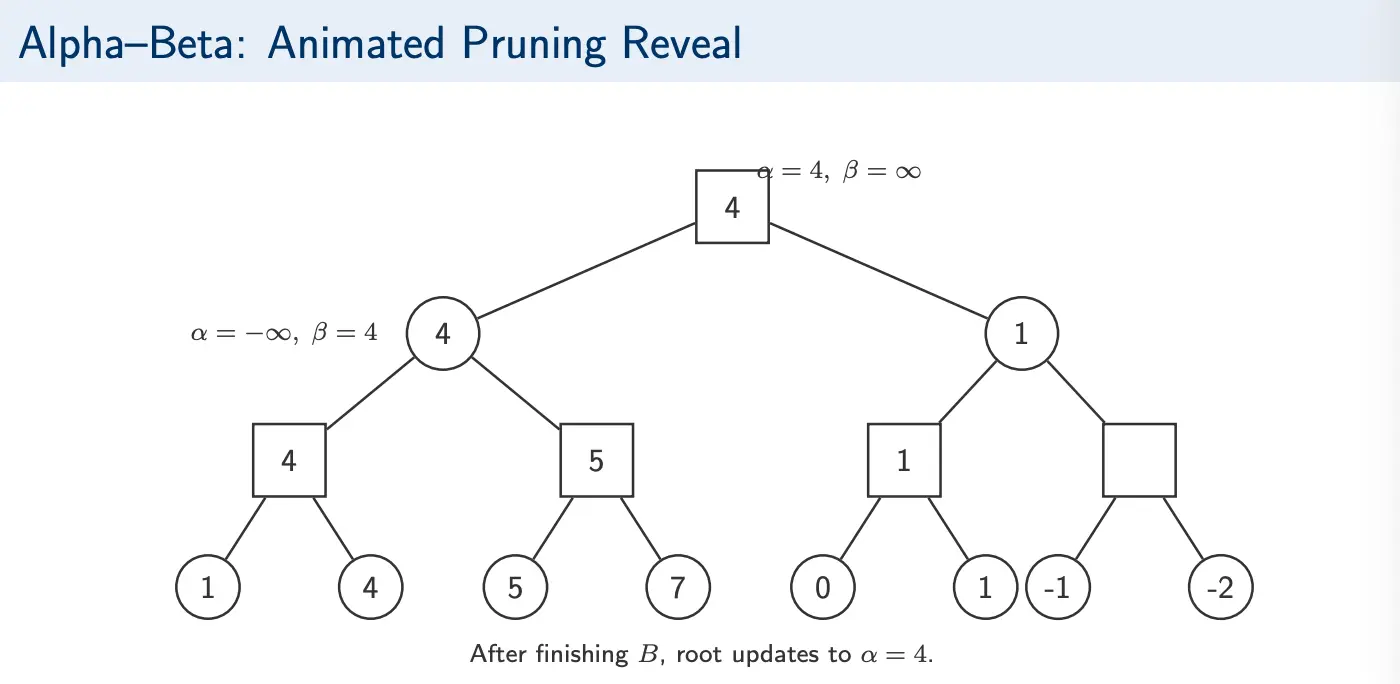
Video Example

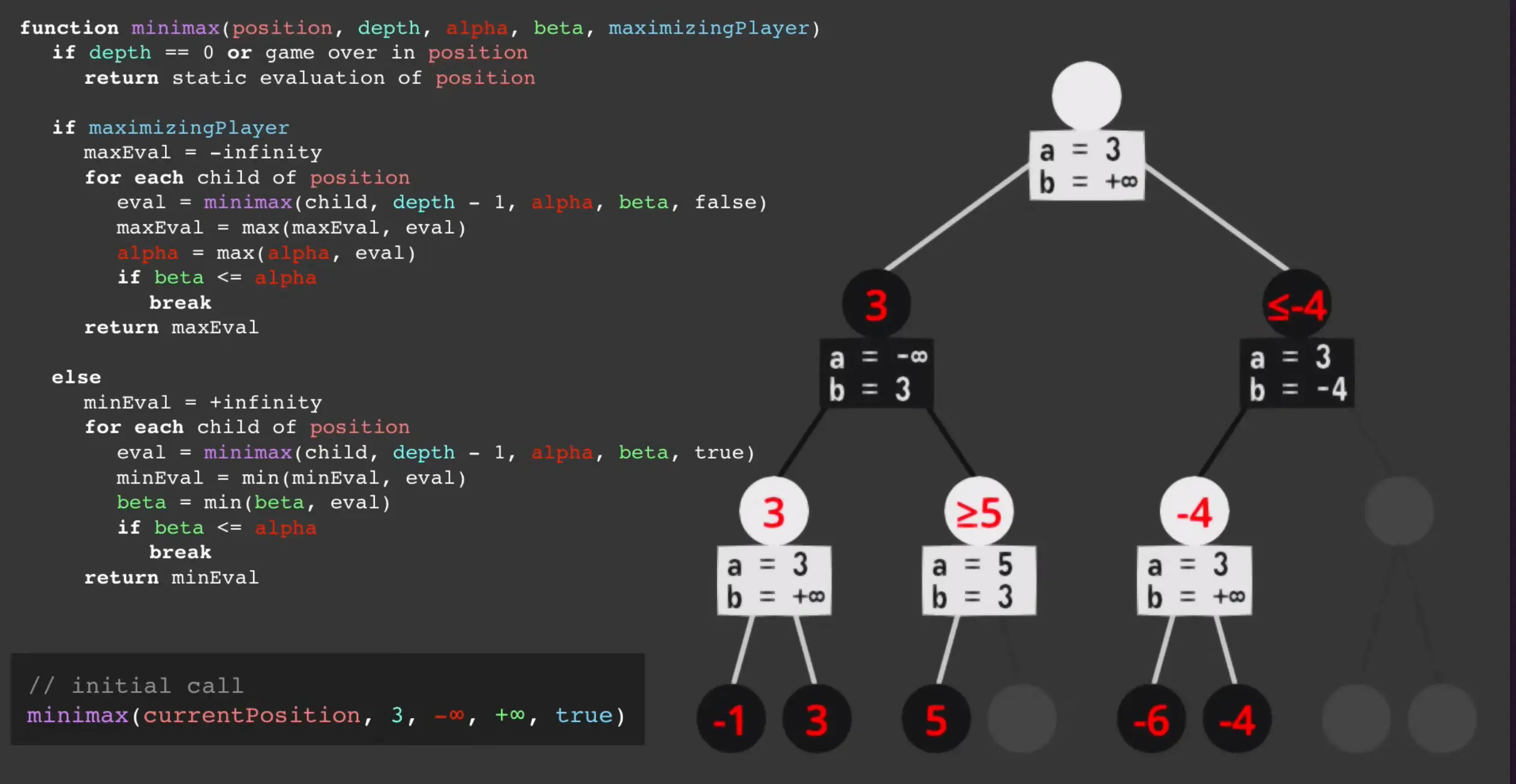
Example 1

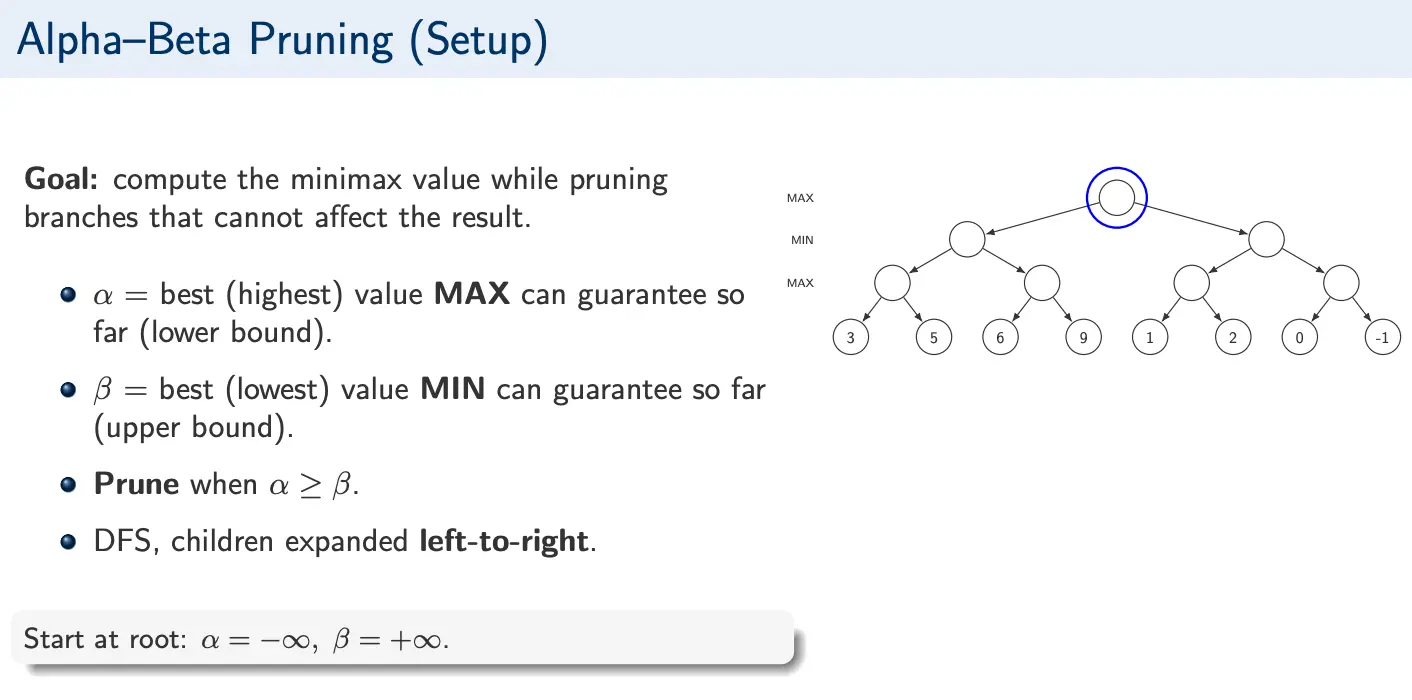
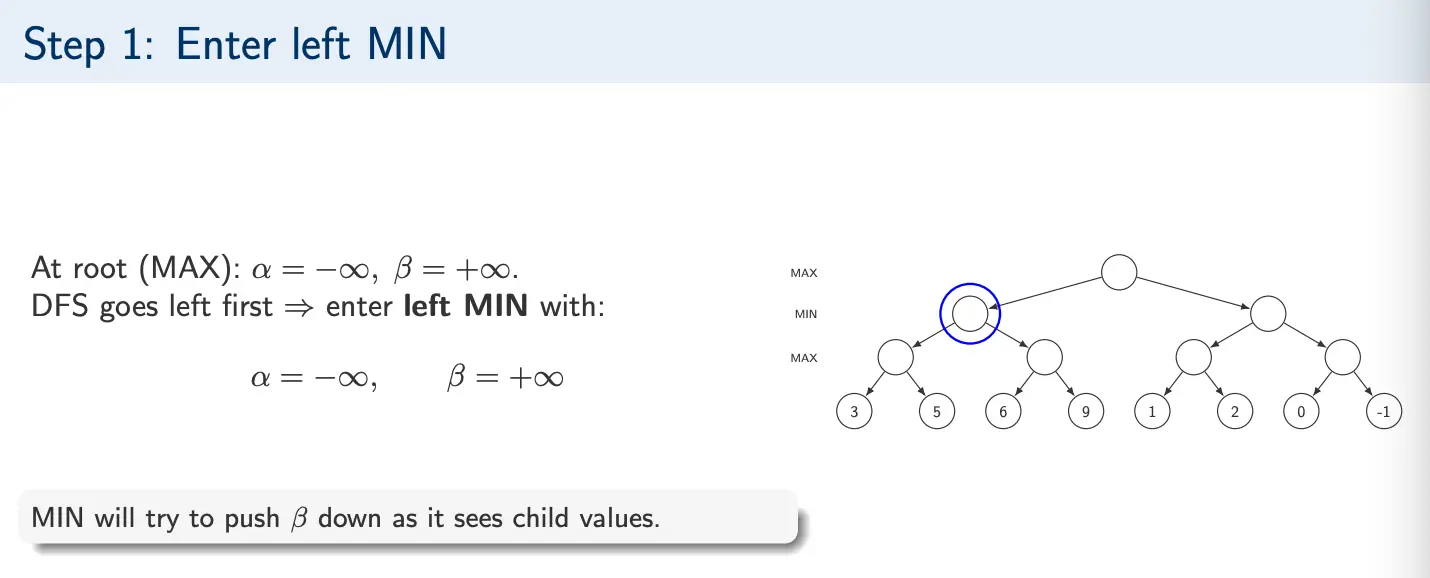
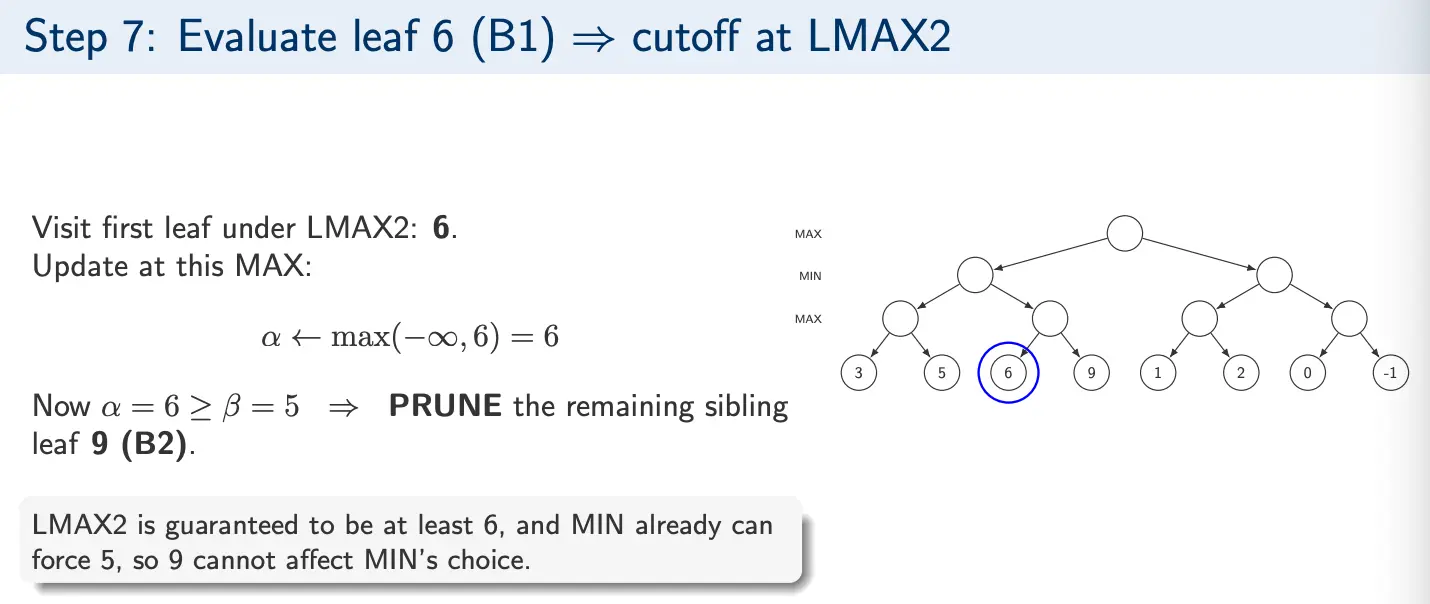
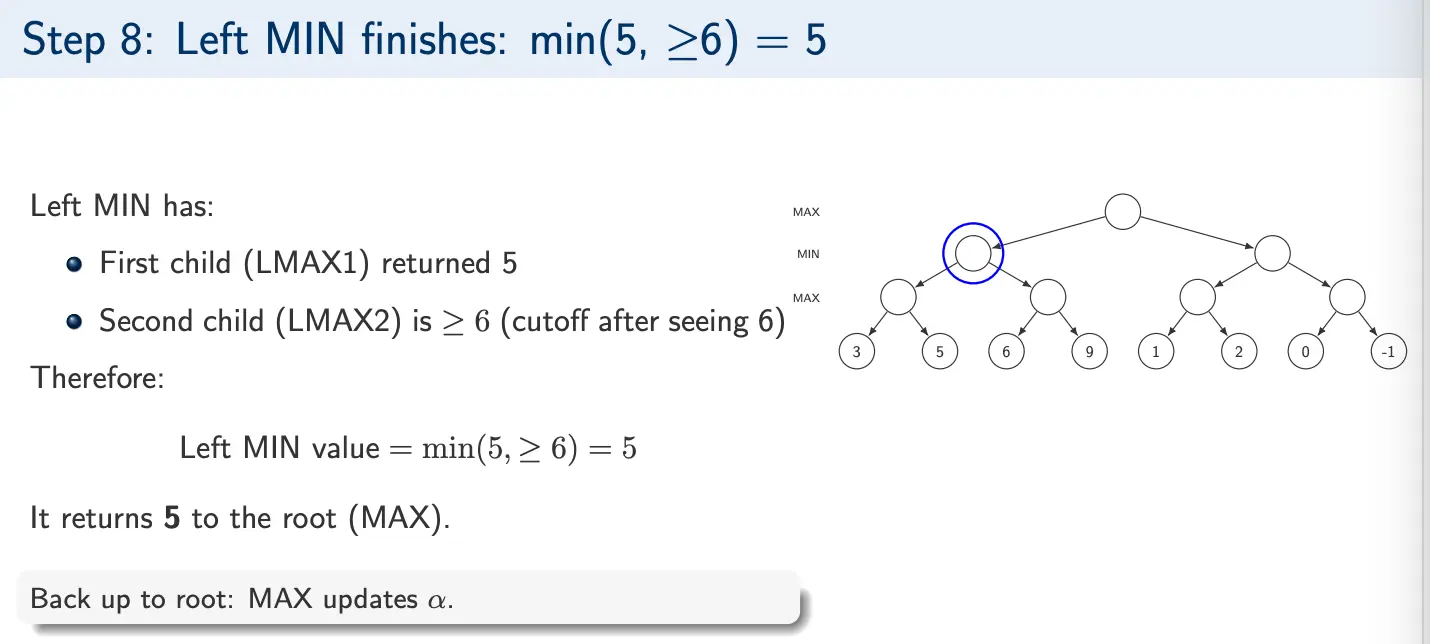
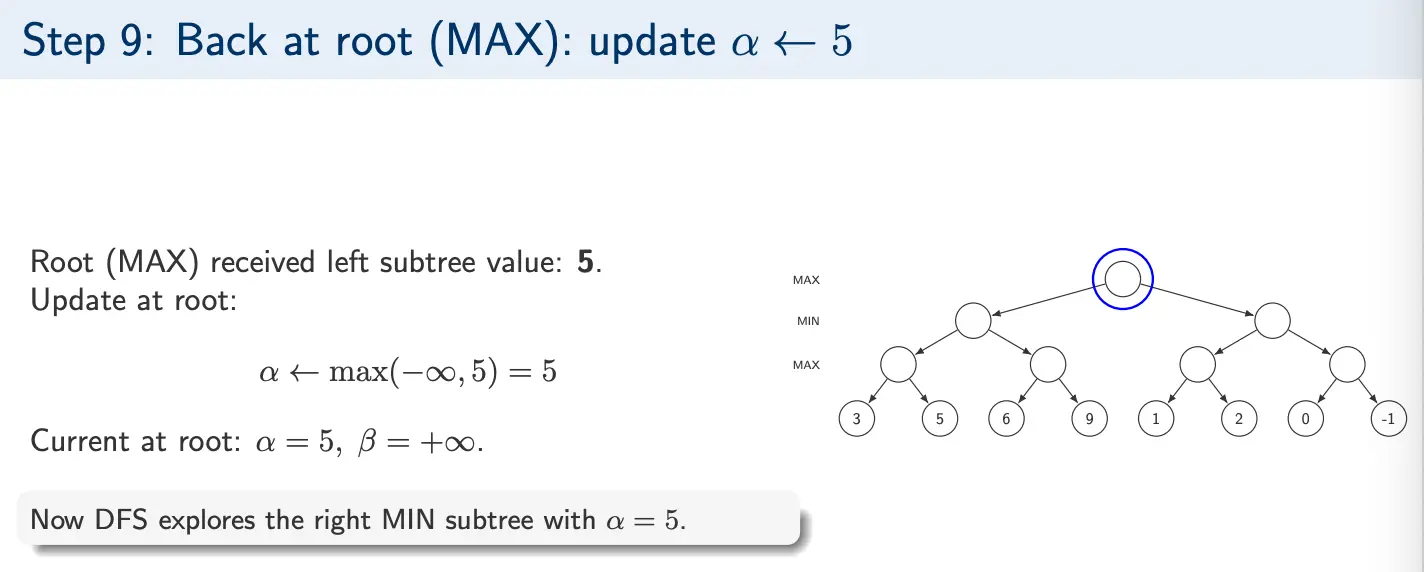
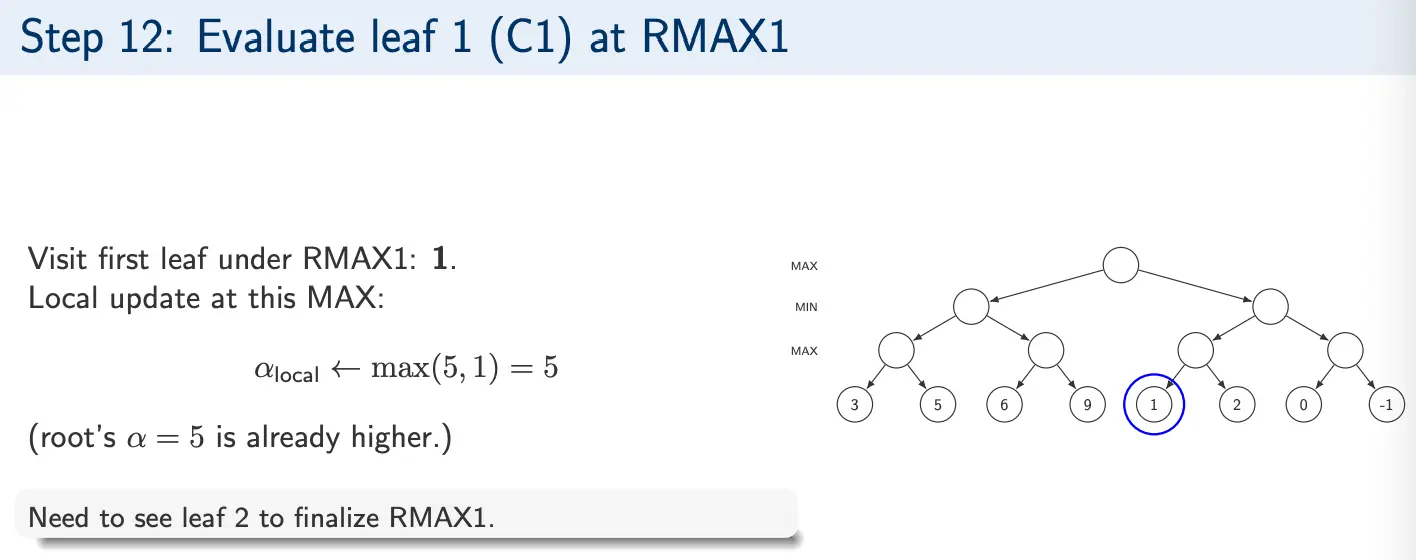
Example 2