Recall that a heuristic is admissible if it never overestimates the true minimal remaining cost to goal:
where is the optimal cost from to a goal. Admissible heuristics are very useful for things like A* Search. They provide an optimistic (may be wrong, but only by being too low), never lying by exaggerating difficulty.
How do we design admissible heuristics? An admissible heuristic is obtained by solving a relaxed version of the original problem. Toward this end, we can remove constraints, allowing more freedom than the real problem, then measure the cost in this easier problem.
This makes intuitive sense; relaxation can only make the problem easier, so the solution cost is a lower bound, which never overestimate.
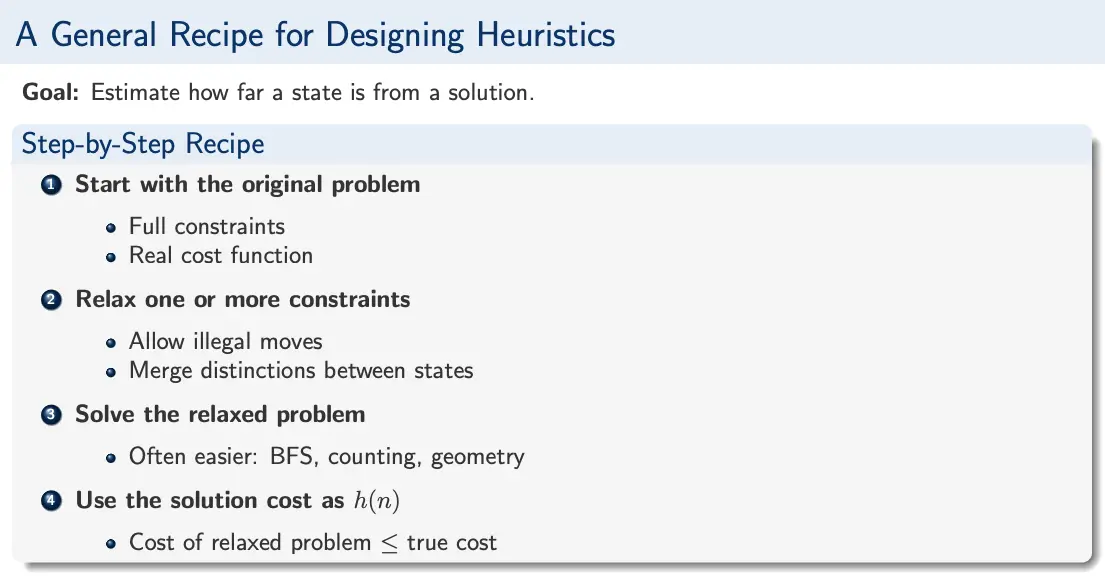
A classic example of a relaxation is grid navigation while avoiding obstacles. Distance metrics like Manhattan distance are a good heuristic to use here; obstacles can only increase the real path cost, so ignoring them makes the problem easier. Note that different relaxations yield different heuristics!