Vortex Flow

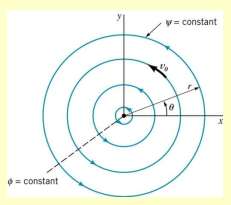
A vortex represents a circular flow around a circular axis. There are two primary types of vortex flows: irrotational (free vortex) and rotational (forced vortex).

Irrotational (Free)

In an irrotational vortex, the fluid particles move in circular paths around a center with no internal rotation (like water swirling in a drain).

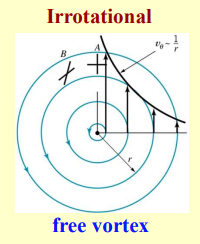
The tangential velocity decreases with radius:

$$V_{\theta }=\frac{1}{r}\frac{\partial \varphi }{\partial \theta }=\frac{K}{r}$$

where $K$ is a constant representing the strength of the vortex.

The radial velocity is simply zero:

$$V_r=\frac{\partial \varphi }{\partial r}=0$$

The velocity potential can be solved to be:

$$\varphi =K\theta$$

• Equipotential lines are radial lines because $\varphi$ varies with the angle $\theta$.

The stream function can be found to be

$$\psi =-K\ln (r)$$

• Streamlines are concentric circles around the origin.

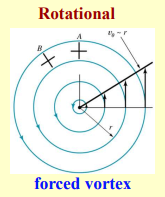
Rotational (Forced)

In a forced vortex, the fluid particles rotate like a solid body; the velocity increases linearly with radius.

$$V_{\theta }=\omega r,V_r=0$$

This type of motion is different from the free vortex because it requires a continuous input of energy to maintain the rotation.

Circulation

Circulation represents the line integral of the tangential component of velocity around a closed path:

$$\Gamma ={\oint }_C\mathbf{V}\cdot d\mathbf{s}$$

For irrotational flows, if there are no singularities:

$$\Gamma ={\oint }_C\nabla \varphi \cdot d\mathbf{s}=0$$

However, if a singularity like a point vortex exists, the circulation is non-zero and is:

$$\Gamma ={\int }_0^{2\pi }\frac{K}{r}rd\theta =2\pi K$$

The velocity potential and stream function expressions become:

$$\varphi =\frac{\Gamma }{2\pi }\theta ,\psi =-\frac{\Gamma }{2\pi }\ln (r)$$

• The streamlines are circular around the center, and the flow remains irrotational everywhere except at the singularity.