Doublet Flow

A doublet flow is a special combination of a source and a sink of equal strength, placed close to each other, and then allowing the distance between them to shrink to zero while keeping the product of their strength and separation constant.

We need:

• Source with positive strength $m>0$
• Sink with negative strength $m<0$

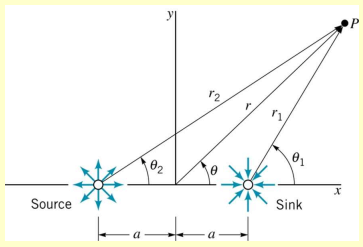
For a standard standard source-sink pair, the stream function in polar coordinates is represented by

$$\psi =\frac{m}{2\pi }\theta$$

However, when they are paired at a small distance, the stream function adjusts to account for the influence of both the source and the sink:

$$\psi =-\frac{m}{2\pi }({\theta }_1-{\theta }_2)$$

The doublet is formed by letting distance $a\to 0$, while keeping $\frac{ma}{\pi }$ constant. We can express the stream function involving the separation distance:

$$\psi =-\frac{m}{2\pi }{\tan }^{-1}\left(\frac{2a\sin \theta }{r^2-a^2}\right)$$

In the limit of very small $a$, this simplifies to

$$\psi =-\frac{mar\sin \theta }{\pi (r^2-a^2)}$$

When $a$ becomes nearly zero, it simplifies to classic doublet form:

$$\psi =-\frac{K\sin \theta }{r}$$

where $K=\frac{ma}{\pi }$ is the strength of the doublet.

From this expression, we know that $c=-\frac{K}{r}$ for a constant streamline. This rearranges to a parametric form:

$$c\sin \theta =r$$

Multiplying both sides by $r$:

$$cr\sin \theta =r^2$$

This is the equation of the circle in polar coordinates!

In Cartesian form, this can be expressed as

$$cy=x^2+y^2$$

Re-arranging, this represents:

$$x^2+{\left(y-\frac{c}{2}\right)}^2={\left(\frac{c}{2}\right)}^2$$

This is the equation of a circle, indicating that the streamlines of a doublet are circular and symmetric about the origin.

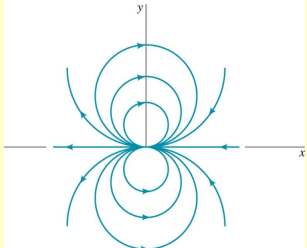
• Fluid is emitted from the source and absorbed by the sink, creating closed circular patterns.
• As the distance a decreases, the flow field around the origin intensifies, leading to the characteristic pattern of a doublet.

The velocity potential for a doublet is given by

$$\varphi =\frac{K\cos \theta }{r}$$

Note that the velocity potential lines ($\varphi =\text{const}$) are orthogonal to the streamlines. - The lines are structured such that fluid moves towards the sink and away from the source symmetrically.